„A tudományos emberfő mennyisége 
a nemzet igazi hatalma.”

Széchenyi István

Gróf Széchenyi István: Hitel

Széchenyi mondását abban a formában idézem, melyben, azt hiszem, először fogalmazta meg a Hitelben. Ezt a mondatot igen sokan idézik, és mindenki egyetért vele. Közhely, hogy Magyarországnak növelnie kellene a hozzáadott értéket termékeiben és szolgáltatásaiban, amit minél több szellemi munka befektetésével, igényesebb, modernebb, csúcstechnológiával előállított termékkel és szolgáltatással tudunk elérni. Ehhez pedig minél felkészültebb, jobban oktatott népességre van szükség. (Sajnos, kevés társadalom jut el addig a következtetésig, hogy azokat a pedagógusokat, akik legfőbb kincsünknek, gyermekeinknek, a legfőbb útravalót, a tudást adják, kellően megbecsülje. De ma az oktatás más problémáiról szeretnék beszélni.)

Természetesen az ördög a részletekben bújik meg: mit, mennyit, hogyan, kinek tanítsunk? Ezeknek a kérdéseknek néhány bonyodalmáról szeretnék beszélni, egy egyetemen oktató matematikus szemével, de igyekszem majd általános dilemmákat felvetni. Beszélni fogok a matematika példáján keresztül arról, hogy egy tudomány milyen vonatkozásai volnának azok, amelyekről egy intelligens embernek képet kellene alkotnia; a növekedés következményeiről és korlátairól. ...

1. Mit kellene tudni matematikából és matematikáról?

Hadd kezdjem néhány olyan ismerettel, amit (úgy érzem) egy intelligens érettségizett embernek tudnia kellene matematikából, illetve, amit tudnia kellene a matematika lényegéről, működéséről, hatékonyságáról. Nem a saját tudományomat akarom földicsérni ezzel: azt szeretném illusztrálni, hogy milyen nehéz dolog akár a saját tudományunkban is kijelölni egy jó tananyagot. (És akkor még a tanítási módszerekről nem is szóltam.)

Hétköznapi számolás • Ez a matematika tanításának azon célkitűzése, amit senki sem vitat. A közoktatás szintjén maradva, természetesen tudni kell az alapműveleteket, meg kell érteni, hogy mi a százalékszámítás, mik a statisztika elemei (például mit jelent, hogy „átlag”), hogyan lehet egy szoba területét kiszámítani, és ide sorolható az egyenletmegoldás is.

Matematikai gondolkodásmód • A mindennapi életben is fontos képesség, hogy egyszerű logikai érveléseket végig tudjunk vinni; hogy több lehetséges esetet meg tudjunk különböztetni; hogy felismerjük, ha bizonyos dolgok között logikai vagy matematikai összefüggés van; hogy leleplezzük az inkorrekt logikát. Ne higgyük azt, hogy a matematikai gondolkodásmód csak matematikusokra jellemző: mindenki így gondolkodik, amikor például sakkozik vagy rejtvényt fejt.

M. C. Escher: Metamorfózis II., fametszet

A matematika él • A tradicionális középiskolai tananyag többé-kevésbé a 17. századi szintig jut el. Azóta olyan fogalmak és eredmények születtek, melyek megalapozták (többek között) a modern fizikát, a mechanikától az atomfizikáig: ide tartozik az analízis, a valószínűségelmélet, csoportelmélet és sok minden más. (Ezeket a megnevezéseket nem ijesztésül szántam, de nyilván kevesen tudják, hogy mit takarnak; ez is mutatja, hogy mennyire szükség volna arra, hogy újabb matematikát is tanítsunk; a nehéz kérdés az, hogy hogyan.)

Vannak olyan matematikai eredmények, melyek megkerülhetetlen hatással voltak a filozófiára is. Ilyen eredményre példa a Bolyai–Lobacsevszij-féle hiperbolikus geometria, mely megmutatta, hogy a térnek nemcsak egyféle fogalma lehet. Itt lehet említeni a matematikai logika területéről Kurt Gödel eldönthetetlenségi tételét, mely ugyancsak fontos filozófiai következményekkel is jár, hiszen azt mondja, hogy még a matematikán belül sem lehet minden megfogalmazható kérdést csak matematikai következtetéssel eldönteni. A matematika kutatása nem záródott le, nagyobb intenzitással folyik, mint valaha!

A matematika hasznossága • Megint más matematikai elméletek teszik lehetővé a számítógépek, az internet, CD-lejátszók, GPS-ek működését, és biztosítják adataink biztonságát. Annak, hogy egy statisztikai tényt hogyan kell értékelni, mennyire megbízható és mennyire szignifikáns, ugyancsak mély matematikai elmélete van. Sok példát lehetne itt még hozni, de inkább áttérek a következő, kevésbé nyilvánvaló pontra.

A matematika szépsége • Mivel az a megtiszteltetés ért, hogy egy művészeti akadémia meghívására tartok előadást, hadd időzzek el a matematika esztétikai kérdéseinél kicsit többet, mint amennyit fő témám, az oktatás indokolna. Furcsa dolog, hogy a matematika területén egy-egy eredmény legfőbb dicsérete nem az, hogy hasznos, fontos, újszerű, hanem az, hogy „szép”. A végső szempont (legalábbis az elméleti matematika területén) esztétikai. Sok idézettel lehetne ezt illusztrálni, én kettőre szorítkozom. Az egyik legfontosabb matematikai kitüntetés, a Fields-érem átadásakor így méltatták Terence Tao munkáját: „Tao és társzerzője, Knutson gyönyörű művet alkotott egy Horn-sejtés nevű problémával kapcsolatban…” A 20. század egyik legnagyobb fizikusa, Richard Feynman írja: „Aki nem ismeri a matematikát, annak nehéz megértenie a természet legmélyebb szépségét…”

Sok minden lehet „szép” a matematikában. Elterjedt nézet szerint az egyik legszebb formula Leonhard Eulertől (a 18. század legnagyobb matematikusától) származik:

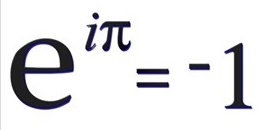Gondolom, aki nem matematikai képzettségű, az felkapja a fejét: Hogy lehet egy formula „szép”? Talán ebben az esetben tudok némi magyarázattal szolgálni: a formula bal oldalán három olyan mennyiség szerepel, melyek a matematika különböző területeiről származnak. Legismerősebb talán a „pi”, a kör kerületének és átmérőjének hányadosa. Az „i” imaginárius egységet, a -1 szám négyzetgyökét az algebrában vezették be, mert segítségével bizonyos egyenletek megoldását elegánsabban lehetett megadni (itt is egy esztétikai jelzőt használtam!). Végül az „e” számot a differenciál- és integrálszámítás sugallta, mert számos kifejezés elegánsabb lett, ha például a szokásos 10 alapú logaritmus helyett az „e” alapú logaritmust használták. Az a tény, hogy három ilyen különböző indíttatással bevezetett mennyiség egyetlen tömör képletben kapcsolódik össze, a matematika egészének mély belső harmóniáját sugallja, és jogosan nevezzük szépnek.

Lehet a matematikában egy tétel bizonyítása is „szép”. Erdős Pál szokta mondani, hogy az Istennek van egy könyve, amelyben minden tételre le van írva a legszebb bizonyítás. Ha valaki elmesélt neki egy bizonyítást, ami nagyon tetszett neki, akkor azzal dicsérte, hogy „ez egyenesen a Könyvből van”. (Két német matematikus, Martin Aigner és Günther M. Ziegler, írtak is egy könyvet Proofs from the Book címmel, mely több, általuk nagyon szépnek érzett bizonyítást tartalmaz.)

Typotex Kiadó, 2004, Szép Magyar Könyv

Az igazi képzőművészetekhez talán azok a geometriai objektumok vannak a legközelebb, amelyeket a legkülönbözőbb matematikai módszerek hoznak létre, és amelyek szemre is igen tetszetősek. Híresek ilyen szempontból a fraktálok, sok szép képet produkált az internet-modellezés, és igen érdekes matematika, a sík különböző szimmetriái vannak a különböző kövezetek hátterében, a leghétköznapibb lépcsőházi mintáktól az Alhambra utolérhetetlen díszeiig. A fraktálok megihlették a költőket is (Ferencz Győző: Fraktál-tudat, URL1), a kövezetek pedig a képzőművészeket, leginkább Maurits Cornelis Escher grafikáira lehet hivatkozni (melyekben fölbukkan a Bolyai–Lobacsevszkij-geometria is, ezzel is illusztrálva ennek a matematikai eredménynek sokirányú hatását). Egyes biológiai alakzatok, virágok, termések pedig már három területet kapcsolnak össze, hiszen a kialakulásuk matematikai és biológiai tények összjátékának köszönhető, szépségük azonban esztétikai jelenség.Tudunk-e mindezekből, a matematika gondolkodásmódjából, élő voltából, alkalmazásaiból és szépségéből bármit is megtanítani, vagy legalábbis megmutatni a fiataloknak? Bár e tekintetben Magyarország talán kicsit előtte jár sok más országnak, amit egy érettségiző az új (ami azt jelenti, hogy csak kétszáz éves!) matematikáról tud, az elenyésző. Ez nem a tantervalkotók hibája: a matematika építkező tudomány, nem lehet az alapokat átugorni.

M. C. Escher

Hadd szemléltessem ezt az utóbbi ötven évben a matematikatanítás filozófiájának változtatásával (mondjuk a középiskolára lehet gondolni, de a történtek átnyúltak az általános iskolába és az egyetemre is). Az 1960-as évekig a hagyományos, évszázadok során kialakult tananyagot oktattuk: sok geometria, egy kevés algebra, geometriai szerkesztések. Aztán a fentiekhez hasonló érvek alapján sor került a tananyag drasztikus modernizálására, „new math” néven Amerikában és Európa legtöbb országában. Sajnos általában nagyon rosszul: egy modern, de érthetetlen, precízkedő nyelvezet lett bevezetve igazi tartalom nélkül. Nem is tartott soká, amíg a reakció elsöpörte, azzal a szállóigévé vált megállapítással: „Why Johnny Can’t Add”. Mint majdnem minden ilyen reakció során, a fürdővízzel együtt a gyereket is kiöntötték, és manapság az amerikai matematikatanítás szinte az egész közoktatásban összeadások és szorzások gyakorlásából áll. Más szóval, a fent említett öt cél közül csak az elsővel foglalkozik.

Meg akarom jegyezni, hogy Magyarországon (és néhány más országban) a „new math” sokkal okosabban és mérsékeltebben lett bevezetve: modern nyelv helyett a modernebb problémákra helyezve a hangsúlyt. Varga Tamás és még sok kiváló matematikus és matematikatanár sok évig dolgozott ezen, és bár a reform itt sem lett teljesen sikeres, sok fontos eleme ma is része a matematikai tananyagnak.

Mindezt elsősorban azért hoztam föl, hogy a tananyag-modernizálás sok problémájára rámutassak: a szakmai kérdések mellett a politikai divatok és a hozzáértő személyek, kutatócsoportok megléte döntő lehet. Hadd jegyezzem meg itt, hogy nagyon aggaszt az, hogy a szakdidaktikai kérdések vizsgálata, az új tananyaggal és módszerekkel való kísérletezés nagyon visszaesett nálunk az utóbbi évtizedekben, elsősorban, azt hiszem, támogatás híján.

2. Növekedés minden téren

... A „középiskolai” tananyag (vagyis az az ismeretanyag, amelyről egy intelligens embernek tudnia kellene ahhoz, hogy a mindennapi életben eligazodjon) robbanásszerűen nő, és nemcsak a matematikában vagy a természettudományokban. Gondoljunk arra, hogy az utóbbi negyven-ötven évben született a számítástechnika; a genetika és molekuláris biológia; az elemirész-fizika; hihetetlen mértékben fejlődött a gyógyszergyártás; hozzáadódott a hagyományos ismeretanyaghoz az utóbbi negyven-ötven év történelme (ami mai helyzetünket közvetlenül meghatározza); negyven-ötven év képzőművészete, zenéje és irodalma (amit a legtöbbet nézünk, hallgatunk és olvasunk); a kitágult világ, a Távol-Kelet, Dél-Amerika kultúrája stb. A decentralizált, privatizált gazdaság miatt szinte mindenkinek szüksége van elemi közgazdaságtanra és statisztikára. A demokrácia és a jogállamiság kialakulása után, ezek megvédése és állandó fejlesztése jogi és államigazgatási alapismereteket igényel minél szélesebb rétegek részéről. Említhetném még a környezetvédelem igen összetett problémáit.

Ugyanakkor a hagyományos anyagrészekről lemondani vagy lehetetlen (mert nélkülük az újabb érthetetlenné válna), vagy legalábbis nagy kárt okozna. Közös probléma ez bármely tantárgy tanításában.

Mit lehet tenni? Belenyugodjunk-e, hogy a jövő értelmisége szükségképpen szakbarbár lesz? Hogy a jövő középosztálya olyan eszközöket, módszereket fog használni, melyek lényegéről fogalma sincs? Hogy a választók és választott képviselőik úgy foglalnak állást például környezetvédelmi kérdésekben, hogy azok tudományos, technikai, jogi és gazdasági alapjairól fogalmuk sincs? Hogy ne tudjunk különbséget tenni tudomány és áltudomány, orvoslás és kuruzslás, statisztikailag jelentős és jelentéktelen adatok között?

Három dolgot látok, ami erre a dilemmára valamelyes választ ad. Nincs varázsszer, nincs örökérvényű megoldás, de ezeket érdemes lenne figyelembe venni.

Az „általános intelligencia” elsajátítását nem lehet az érettségivel befejezettnek tekinteni. Tehát a felsőoktatásban a hagyományos szakképzés mellett fontos helye kell, hogy legyen az általános képzésnek is. ...

Fel kell készíteni mindenkit a folyamatos, „holtig való” tanulásra. Vannak ezen a téren igen jó hagyományaink: ismeretterjesztő hetilapok és folyóiratok, előadás-sorozatok (mint például amilyen a Mindentudás Egyeteme volt). Örvendetes, hogy szaporodnak az ismeretterjesztésre specializálódott TV-csatornák (repesett a szívem, amikor unokáim a piff-puff rajzfilmekről átkapcsoltak a sarkvidéki állatokat bemutató ismeretterjesztő filmre, mert az szerintük érdekesebb volt).

Lovász László a MindenTudás Egyetemén 2003-ban

De az így elérhető témák választéka eléggé esetleges, főleg a nehezebben kommunikálható témákban, mint például a matematika. A természettudományok és a társadalomtudományok területén sok olyan érdekesség van, amit el lehet mesélni, ahonnan el tud indulni egy ismeretterjesztő előadás vagy film. Ilyen lehetőséget nyújt a természetfilmek, múzeumok mellett akár a történelmi és tudományos-fantasztikus irodalom is.Matematikából sokkal nehezebb a helyzet, és gondolom, hogy más tudományok, tudományágak is vannak ugyanilyen nehéz helyzetben. A nemzetközi matematikai közéletben csak az utóbbi egy-két évtizedben erősödött meg az a felfogás, hogy a matematika eredményeit, problémáit is kommunikálni kell a széles közvélemény számára. Ehhez a matematika belső szépsége mellett a sikeres alkalmazásai is használhatók az érdeklődés megragadására. Itt távolról sem értük el azt a szintet, amit szeretnénk, mert sok aprómunkára, igen sok példa és illusztráció kidolgozására lesz még szükség. Örülök annak, hogy kezd kialakulni az együttműködés képzőművészekkel és talán zeneművészekkel, írókkal is.

Mindez azonban nem ad választ arra, hogy mit tanítsunk, mondjuk, a középiskolában. Azt gondolom, ki kellene dolgozni olyan kompromisszumos megoldásokat, melyek lehetővé teszik, hogy a diákok megtanulják az alapokat, de azt is, hogy valamennyire bemutassuk, valamilyen szinten tanítsuk a tudomány legújabb eredményeit is. Ez talán a matematikában a legnehezebb, mert ennek a tudománynak lényege az egzaktság, minden állítás minden szavát pontosan kell definiálni, és minden állítást be kell bizonyítani. Ha felületes, az eredményeket pontatlanul kimondó és bizonyítás nélkül hagyó ismeretanyagot akarna valaki tanítani, ez ellen szinte egy emberként tiltakozna a matematikusok közössége. Mégis, valami ilyesmire volna szükség, hogy az iskolából kikerülőknek képük legyen a matematika szépségéről, erejéről, hasznosságáról; hogy ne kezdődjön egy kívülálló és egy matematikus beszélgetése azzal az obligát mondattal, hogy „én mindig hülye voltam a matematikához”. Ilyen tananyagok, tanítási módszerek kidolgozása persze nekünk, matematikusoknak, matematikát tanítóknak a dolgunk, de a társadalom nagyobb nyitottsága serkentően hatna. ...

 „Egy nemzet ereje a kiművelt emberfők sokaságában rejlik” (hogy Széchenyi gondolatát ismertebb formájában idézzem), de nem mindegy, hogy hogyan, mire műveljük ki ezeket az emberfőket. A jó oktatás kialakítása és szinten tartása minden területen állandó gondolkodást, kísérletezést, vitát igénylő feladat, és csak remélni tudom, hogy ehhez a munkához meglesz a kellő türelem, pénz, szaktudás és politikai támogatás.  

MTA Díszterem

A Széchenyi Irodalmi és Művészeti Akadémia IV. Széchenyi István emlékestjén, 2013. április 9-én, az MTA Dísztermében elhangzott beszéd szerkesztett változata.

Forrás: http://www.matud.iif.hu/