Mindentudás Egyeteme, 2003.

I. Bevezetés

A számítógépek a 20. század igazi forradalmát jelentik. Az elmúlt évszázad második felét szokás „atomkorszakként” emlegetni; azonban pontosabb leírás volna a „számítógépek korszaka”. Akár egy évnyi előadássorozatot is össze lehetne állítani a számítógépek, az információs technológia hatásáról a kultúra és a tudomány különböző területein. Ez az előadás csak a matematika szempontjából veszi szemügyre a számítógépeket.

Legjobb, ha mindjárt az elején felhívom a figyelmet valamire. A matematika az egzakt gondolkodásról szól, és nem lehet matematikáról anélkül beszélni, hogy legalább egy kicsit ne kóstoljunk bele ebbe az egzakt gondolkodásba. Elkerülhetetlen tehát, hogy a hallgatókat, olvasókat legalábbis időnként arra kérjem, hogy együtt gondolkozzunk, hogy ne csak a tényeket, hanem azok logikáját is kövessék.

Mindjárt föl is teszek egy kérdést, mely gyakran fölvetődik, és melyre az első, átgondolatlan válaszunk könnyen az igazság ellenkezője lehet: Feleslegessé teszik-e a számítógépek a matematikát?

Minden nagy fejlődés sok olyan dolgot tesz fölöslegessé, mely korábban fontos, sőt alapvető volt. Odakerül-e a matematika is a logarléc és a gőzmozdony mellé? Látni fogjuk, hogy éppen ellenkezőleg, a számítógépek igénye a matematika új fejezeteit hívja létre és a régi fejezeteket egészen új megvilágításba helyezi. A számítógép új kérdéseket tesz fel a matematikának, és ezek a kérdések új fogalmak, új paradigmák kialakulásához vezetnek.

A probléma gyakran konkrétabb formában is megfogalmazódik: Nem teszi-e feleslegessé a hardver fejlődése a matematikai módszereket a programozásban? A hardver hihetetlen fejlődésen ment és megy keresztül.

Gordon E. Moore

Ezt a fejlődést Moore törvényével lehet leírni. Gordon E. Moore az Intel egyik alapítója, és 1965-ben azt a megfigyelést tette, hogy az egy-egy integrált áramkörben használt tranzisztorok száma mintegy 2 évenként megduplázódik. Ez a gyors fejlődés azóta is tart. 

Neumann János a számítógépek egyik atyja. A háttérben levő gépen jól láthatók a rádiócsövek; minden ilyen cső egy-egy számítási alapegységet, „kaput” valósít meg. Ma egy négyzetcentiméteren 50 millió ilyen kapu van!

Sok az olyan feladat, amelyet csak nehezen, bonyolult trükköket bevetve tudunk megoldani, de egy évvel később a sokkal gyorsabb, nagyobb kapacitású gépek játszva megcsinálják őket. Úgy tűnhet tehát, hogy kár a bonyolultabb matematikai módszereket erőltetni. Ám ha jobban megnézzük, kiderül, hogy éppen ellenkezőleg: a technikai fejlődés olyan feladatokat hoz létre, amelyeket „trükkös” gondolkodással már nem lehet megoldani, csak komoly matematikai módszerekkel.

Meg lehet-e érteni például egzakt matematikai gondolkodás nélkül az internetet, amely több százmillió számítógépet köt össze egymással? Meg lehet-e tervezni egzakt matematikai módszerek nélkül egy modern integrált áramkört, ahol 50 millió számítási alapegység van egy négyzetcentiméteren összezsúfolva? Lehet-e pontos matematikai modellezés nélkül gondolkodni egy olyan rendszer biztonságáról, amelyet milliárdnyi ember használ, akiket nem ismerünk - de tudjuk, hogy vannak köztük bűnözők és terroristák is?

A matematika tehát nagyon is sokat tud nyújtani a számítástechnikának. De mit kap cserébe? Nagyon sok mindent: izgalmas új fogalmakat, problémákat és módszereket, új kísérletezési lehetőségeket. Ezek közül nézünk meg egy párat a következőkben.

II. A bonyolultság új fogalma

A bonyolultság fogalma hasonló fejlődésen ment át az utóbbi 50 évben, mint sok más alapvető fogalom. Először egy megértést akadályozó körülményt jelentett – vagy talán csak kényelmes kifogást? Ha egy jelenség vagy struktúra túl bonyolult, akkor a kutatás során megkerüljük, leegyszerűsítjük vagy részeire bontjuk. A fogalom történetében a következő fázis, amikor a tudós elkezdi a bonyolultságot mint önálló jelenséget szemlélni: kidolgozza, hogyan lehet mérni, szabályokat és törvényeket állapít meg, kapcsolatba hozza más, korábban megismert dolgokkal. Végül jelentkezik a mérnök, hogy a bonyolultságot eszközként használja fontos tervezési problémák megoldására: az adatvédelem, az elektronikus posta, a kereskedelem, a pénzforgalom biztonsága ma nagyrészt a bonyolultság fogalmán és annak tulajdonságain alapul.

A 19. századi matematika egyik nagy sikere a végtelen fogalmának megragadása volt. Ennek bűvölete olyan erős, hogy hajlamosak vagyunk mindenre, ami véges, rálegyinteni: „Véges sok eset van, amit végig lehet nézni!”. A számítógépek megjelenése azt eredményezte, hogy rájöttünk: a véges nagyon nagy is lehet, bekövetkezhet az „exponenciális robbanás”.

1. Exponenciális robbanás

A sakkjáték feltalálójáról szóló klasszikus történet szerint az unalma elűzéséért hálás király felajánlotta neki, hogy azt kívánhat jutalmul, amit akar. A feltaláló azt kérte, hogy a sakktábla első mezejére tegyenek egy búzaszemet, a másodikra kettőt, a harmadikra négyet, a negyedikre nyolcat, és így tovább, minden mezőre kétszer annyit, mint az előzőre. A király nagyon megörült, hogy ilyen olcsón megúszta, de aztán rá kellett jönnie: nemcsak, hogy a 10-12-ik mezőtől már nem férnek el a búzaszemek, de a tábla közepe táján már birodalmának teljes búzatermése sem lett volna elegendő, hogy ígéretét betartsa.

Ezt a jelenséget, hogy ha egy mennyiséget ismételten duplázunk (vagy bármilyen egynél nagyobb számmal szorzunk), akkor igen gyorsan növekszik, exponenciális robbanásnak hívjuk. Moore említett törvényében az a meglepő, hogy az informatikában bekövetkezett exponenciális robbanás ilyen sokáig tud tartani. Az 1960-as évek környezetvédelmi forradalma mögött az áll, hogy egyre többen megértették: az exponenciális növekedés sem a népesség, sem a termelés, sem a fogyasztás területén nem tarthat örökké.

A számítástudományban az exponenciális robbanás leggyakrabban akkor lép fel, ha azt a kijelentést, hogy „Véges sok eset van, amelyet végig lehet nézni!”, megpróbáljuk közelebbről vizsgálni. Mondjuk, az esetek megkülönböztetéséhez először is két alapesetet kell megkülönböztetnünk; aztán ezek mindegyikén belül két újabb eset van stb. Ezt a logikai helyzetet az alábbi ábrán látható hálózattal, ún. bináris fával ábrázolhatjuk.

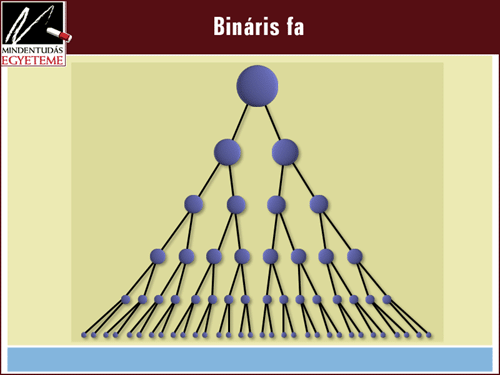
Látható, hogy a végignézendő esetek száma már néhány elágazás után is ugrásszerűen nő, és bekövetkezik az exponenciális robbanás. Ha algoritmusunk egy ilyen fát kell hogy végigvizsgáljon, akkor a modern számítógépek mondjuk 30 szint mélységig még bírják, csakhogy minden egyes újabb szint megduplázza az esetek számát. Itt még Moore törvénye sem segít: ha 10 évig várunk, akkor mondjuk 5 szinttel tudunk továbbmenni.

Ezért aztán a számítástudományban elég hamar megfogalmazódott, hogy olyan algoritmusok tervezésére kell törekedni, amelyek lépésszáma a feladat méretével csak mérsékelten nő, úgy, mint a méret egy hatványa, nem pedig exponenciálisan. Tehát ha a feladat mérete n, akkor a lépésszám lehet n2 vagy n3, de nem lehet 2n. Az ilyen algoritmust polinomiálisnak szokás nevezni. A kétfajta növekedés közötti különbséget úgy lehet legjobban szemléltetni, ha elgondoljuk, hogy mekkora teljesítménynövekedést lehet várni a technológia fejlődésétől. Tegyük fel, hogy mind az A algoritmus, mind a B algoritmus ma 50 bemenő adattal tud egy adott problémát megoldani. Az A algoritmus lépésszáma úgy nő a bemenő adatok számával, mint n3, a B algoritmusé, mint 2n. Ha várunk 10 évet, és a számítógép teljesítménye 32-szer akkora lesz, mint ma (Moore törvénye szerint), akkor az A algoritmus már 150 bemenő adattal bír el, míg a B algoritmus teljesítőképessége csak 55 adatra emelkedik.

A folytatás itt olvasható.