A matek egyszerű rejtvényei
Richard Schwartz matematikus elmagyarázza, miért szereti az olyan problémákat, amelyek megoldásába azonnal bele tud fogni, és hogy a számítógépek hogyan segíthetik a kutatást.
 Richard Schwartz
Richard Schwartz
A matematika fontos felfedezéseinek többsége évtizedes vagy évszázados erőfeszítések után születik meg. Ha bele akarunk kezdeni a legnagyobb problémák megoldásába, sok szakmai anyagot kell elsajátítanunk, mielőtt valami újat kezdenénk közölni.
Richard Schwartzot nem érdeklik az ilyen kérdések. Szereti az olyan problémákat, amelyekről ha ma kezd el olvasni, holnap már bele is kezdhet a megoldásukba – az egyszerű, szórakoztató problémákat, amelyekben van valami karneváli játékokból: lássunk neki, és nézzük meg, mi sül ki belőle! Ezt a kutató matematikusok körében ritka hozzáállást Schwartz teljes mértékben felvállalja: „Nem hiszem, hogy érett a hozzáállásom a matematikához”.
Mindez persze nem jelenti azt, hogy Schwartz nem komoly és teljes értékű matematikus. Doktori fokozatát a Princeton Egyetemen szerezte Bill Thurstonnak, az elmúlt fél évszázad egyik legkiemelkedőbb matematikusának a mentorálása alatt.
Schwartz jelenleg a Brown Egyetem professzora. Legfontosabb munkája a dinamika területén olyan iteratív folyamatokat vizsgál, amilyen például egy súrlódásmentes asztalon lévő billiárdgolyó mozgása. 2008-ban bebizonyította, hogy minden 100 fok alatti szögekkel rendelkező háromszög legalább egy periodikus biliárdutat tartalmaz – azaz olyan ismétlődő utat, amelyet egy golyó örökké követni fog.
Schwartz munkája során gyakran használ számítógépes kísérleteket – sőt, e tekintetben élen jár. Ahogy magyarázza, a számítógépek többféle módon is kiegészítik az ember matematikai gondolkodását. Például mintázatokat rajzolnak ki. A mintázatok azután tippeket adhatnak, amelyek akár olyan bizonyítékokhoz is elvezethetnek, amilyenek a számítógép segítsége nélkül talán soha nem jutnának eszünkbe.
A Quanta Magazine arról beszélgetett Schwartzcal, hogy miért kedveli az egyszerű problémákat, amelyeket egyébként a matematika „csodáinak” nevez.
Mit szeret a matematikában?
Mindent szeretek benne. Először is tetszik nekem, hogy működik valahogy. Szeretem, hogy van módszere, így haladást érhetünk el benne. Szeretem, hogy el lehet jutni a kérdések legmélyére, ellentétben a politikával vagy a vallással, ahol akár évekig is beszélhetünk az emberekkel, senki nem fogja megváltoztatni a másik véleményét.
Egyszerűen szeretem az idomokat és a számokat, hogy miért, azt pontosan nem tudom megmagyarázni. Aztán tetszik az intellektuális kihívás. Szeretek megoldani olyan problémákat, amelyekkel mások nem boldogultak. Van ennek egyfajta hegymászás jellege. Végül szeretem a tiszta matematika szépségét, ugyanúgy, ahogy sok ember a műalkotásokét.
Azt mondta, szereti az egyszerű problémákat. Miért?
Először is úgy érzem, hogy ha ez egy egyszerű probléma, amelyet még nem sikerült megoldani, valószínűleg rendelkezik valamilyen rejtett mélységgel. Vagyis az emberi tudásból hiányzik valami, és ez akadályozza meg az embereket a probléma megoldásában.
Másodszor, szeretem a számítógépes kísérleteket: úgy érzem, általuk megvan az esélyem a fejlődésre. A modern számítógép új eszköz, és ezekre az egyszerű problémákra úgy gondolok, mint amelyek alibit kínálnak az adatgyűjtésre. Csak elkezdem programozni a számítógépet, és megpróbálkozom néhány kísérlettel, hátha fel tudok tárni olyan rejtett mintázatokat, amelyeket senki más nem látott csak azért, mert még nem végzett ilyen kísérleteket.
Amikor az ember fiatal, az a benyomása, hogy szinte mindent tud. Most már az az érzésem, hogy a matematikában szinte minden ismeretlen.
Harmadszor, bár ez talán kissé bután hangzik, az általam kedvelt egyszerű problémák nem igényelnek sok hátteret. Szeretem azokat a dolgokat, amelyekkel azonnal elkezdhetek foglalkozni. Türelmetlen vagyok. Ha valamilyen sejtésről hallok a matematika valamely fantasztikus területén, lusta vagyok bíbelődni vele. Nagyon idegen tőlem, hogy hat hónapot töltsek az irodalom olvasásával, amíg el nem érek arra a pontra, ahol készen állok a munka megkezdésére. Szeretek csak kicsit belekóstolni és máris belevágni.
Tudna-e példát mondani ilyen egyszerű problémára?
Az egyik probléma, amely nagyon érdekelt, a háromszögben mozgó biliárdgolyók problémája volt. A kérdés: ha egy háromszögben biliárdgolyókat nézünk, van-e olyan periodikus biliárdút, amely újra és újra ugyanazt a pályát követi? Ez hegyesszögű háromszögekre már ismert volt [ahol az összes szög nem nagyobb, mint 90 fok], de nem volt ismert a tompaszögű háromszögeknél [ahol az egyik szög nagyobb, mint 90 fok]. A kérdés az, hogy van-e minden háromszögben periodikus biliárdút? Tettem némi előrelépést ebben. Bebizonyítottam, hogy amennyiben minden szög kisebb, mint 100 fok, van periodikus biliárdút.
Mondana még egy példát?
Egy másik dolog, amivel elég sokáig foglalkoztam és megoldottam, a külső biliárdgolyók problémája. Adva van egy konvex idom a síkban, mint egy ovális, négyszög vagy ötszög. Kezdjük egy olyan ponton, amely kívül esik az idomon, és… nos, talán rajzolnom kellene.
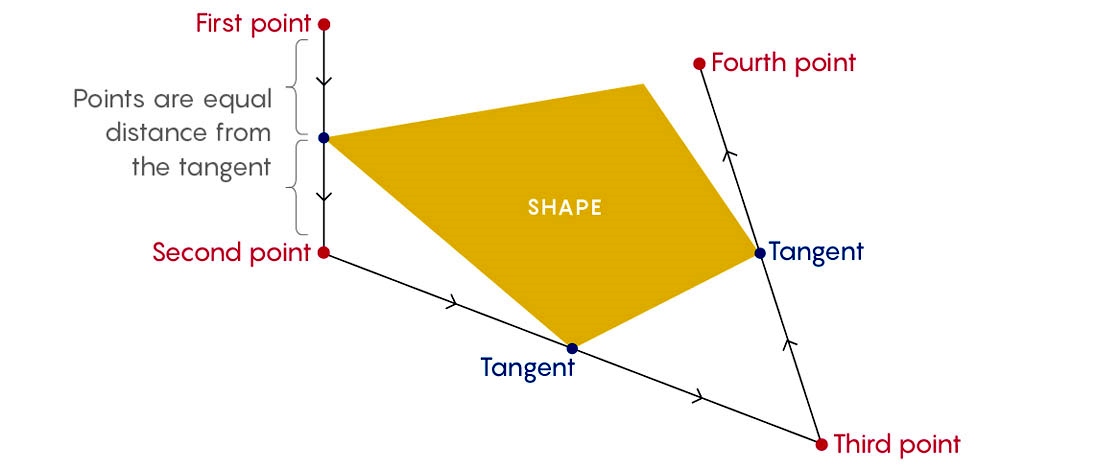 Kezdjük a kiindulási ponton, majd rajzoljunk egy olyan vonalat, amely érintője az idomnak – az idomot egyetlen ponton érinti. Álljunk meg egy olyan ponton, amely egyenlő távolságra van az eredeti ponttól és az érintési ponttól. Ezután ismételjük meg a folyamatot, hogy létrehozzunk valami pálya-szerűt.
Kezdjük a kiindulási ponton, majd rajzoljunk egy olyan vonalat, amely érintője az idomnak – az idomot egyetlen ponton érinti. Álljunk meg egy olyan ponton, amely egyenlő távolságra van az eredeti ponttól és az érintési ponttól. Ezután ismételjük meg a folyamatot, hogy létrehozzunk valami pálya-szerűt.
A fő kérdés végig ez volt: van-e olyan idom és kiindulási pont, hogy a pont tetszés szerinti távolságra kerül az idomtól? Kötetlen-e a pálya? Ez a kérdés megoldódott. Megmutattam, hogy bizonyos idomoknál – mint amilyenek a kétoldalú szimmetriával rendelkező négyszögek – igen, azaz el lehet menekülni.
Meséljen arról, hogyan használja a számítógépet a munkájában, és miért vonzódik ehhez a módszerhez.
Például mert hihetetlenül jó firkapapír. A matematikusok, még a régi nagyok is, mint Gauss és Euler, próbáltak kísérleti bizonyítékokat gyűjteni. Megpróbáltak különleges eseteket kidolgozni, persze papíron és kézzel, hogy némi képük legyen arról, mik a várható eredmények. Bizonyos értelemben a számítógép segítségével sokkal több ilyesmit vihetünk véghez. Lehetővé teszi számunkra, hogy több kísérleti bizonyítékot gyűjtsünk össze a feltételezett igazság mellett.
A számítógép vizualizációs eszköz is. Olyan dolgokat tár fel, amelyek igazságáról nélküle fogalmunk sem lenne. Jó példa arra, hogy valóban szükség van a számítógépre, a Mandelbrot-halmaz. Ha nincs számítógép, kézzel rajzolhatunk néhány pontot. De csak amikor az emberek elkezdték ezeket a számítógépes kísérleteket, derült ki ez a rengeteg információ arról, hogy mi minden van itt: a Mandelbrot-halmaz, a Julia-halmaz és mindazok a dolgok, amelyeket roppant sok számítás és grafikus ábrázolás nélkül nem lehetett volna látni.
 Julia-halmaz
Julia-halmaz
Vannak olyan módszerek, amelyekkel a számítógép lehetővé teszi, hogy minőségileg különböző problémákat oldjunk meg?
Csak annyit mondhatok informálisan, hogy a matematika rendkívül jó a minél szimmetrikusabb objektumok számára. Bizonyos értelemben a matematika csodákról szól. Közelmúltbeli nagy példa erre a Kepler-sejtés Maryna Viazovska-féle, 8 dimenziós megoldása. [A sejtés a gömbök legszorosabb összerakási módjával foglalkozik.] Furcsa, hogy a Kepler-sejtés nyolc dimenzióban sokkal könnyebben megoldható, mint háromban. Ennek oka, hogy nyolc dimenzióban ez a csodálatos gömb-pakolás rendkívül szimmetrikus. E különleges konfigurációk nyolc dimenzióban, na ezek a csodálatos dolgok.
Elmondaná bővebben, mit ért az alatt, hogy a matematika úgy van szervezve, hogy megtalálja a legszimmetrikusabb vagy a legszebb tárgyakat?
Ez majdnem olyan, mintha a matematika nekiindulna, és azonnal kiválasztaná a legragyogóbb, legszebb tárgyakat. Mint a logaritmus, vagy a nulla, vagy az exponenciális függvény. És a geometriában vannak olyan dolgok, mint a vonalak és a síkok. És később sokrétűbb dolgok, ívelt terek és furcsaságok, mint a sémák, amelyeket nem igazán értek jól. A matematika e különleges kanonikus tárgyakra hangolódik rá. Azt mondhatnánk, hogy ezt kellene a matematikusoknak csinálniuk – többet találni ezekből a dolgokból, több drágakövet. Ám ezek a finom drágakövek először olykor nagyon durváknak látszanak.
És a számítógépek segíthetnek megtalálni ezeket a finom drágaköveket?
Hogyne, ez volt a tapasztalatom a külső biliárdgolyók problémájával. Először a külső biliárdgolyók által egy deltoidon előállított mozgás teljesen zajokkal terheltnek és nehezen érthetőnek tűnt, de az adatok reprezentálásának különböző módjaival ezt ki tudtam játszani. Végül az az ötletem támadt, hogy megrajzolom egy magasabb dimenziójú ábrázolással, és hirtelen ez a gyönyörű minta jelent meg. Sosem gondoltam volna rá.
 Fraktál óra Schwartz otthoni dolgozószobájában
Fraktál óra Schwartz otthoni dolgozószobájában
A számítógép nagy mennyiségű információt gyűjthet össze, grafikusan rendezheti a dolgokat, külső memóriánkként szolgálhat, így segíthet felismerni ezeket a mögöttes mintákat, amelyek túl távol állhatnak tőlünk ahhoz, hogy segítség nélkül észrevegyük őket. A számítógép egy sörétes puska megközelítés, csak meg kell próbálni egy csomó dolgot. Bizonyos értelemben egyáltalán nem használjuk az agyunkat, legalábbis eleinte. De aztán kapunk valami visszajelzést, és a kísérletet ehhez igazítjuk. És ha sikeres lesz, akkor tényleg megtudunk valamit, amire magunktól soha nem jöttünk volna rá.
Számos gyermekkönyvet írt a matematikáról. Mi motiválta erre?
Két dolog. Amikor a gyermekeim kicsik voltak, tanítani akartam őket. Kezdtem egy rövid könyvvel a prímszámokról a lányomnak, Lucy-nak. De aztán tovább vittem a projektet, és végül egy hosszú könyvet írtam, a You Can Count on Monsters-t (Számíthatsz a szörnyekre). A kisgyermekek társasága egyébként is nagyon inspirál. A másik motiváció az, hogy szeretek rajzolni. Nem mintha különösen jól rajzolnék, de a számítógépes grafikát kifejezetten kedvelem.
Szeretem a kreatív foglalatosságokat a matematika mellett; szünetet tarthatok a szokásos kutatásomban. Szeretem a nagyobb közönséget is. Mint a legtöbb matematikus, olyan problémákon dolgozom – még ha sikerül is ezeket megoldani – amelyeket nem sokan értenek. Ezzel szemben a képeskönyveimet több ezer ember olvasta már, ami azért nem rossz érzés.
Egy új gyermekkönyvön dolgozik: Life on the Infinite Farm. Mit akar közölni a gyerekekkel a végtelenségről?
Amikor gyerek voltam, magam is sokat gondolkoztam a végtelenségről: milyen lenne, ha végtelen hosszú karom lenne, vagy ha egy asztal végtelen lenne. Úgy gondoltam, a gyerekeknek ez tetszeni fog. A végtelenség egy rendkívül érdekes fogalom.
Néhány ábra a Life on the infinite farm című könyvbőlFord., szerk.: Jakabffy Éva