Milyen mikroszkopikus folyamatok irányítják az állatok kültakaróján a motívumok megjelenését? A modern számítástudomány atyja, a "kódfejtő" Alan Turing 1952-ben felvetette, hogy a diffúzió kémiai törvényei magyarázatul szolgálhatnak például a zebra csíkjaira vagy a jaguár foltjaira.

Turing elmélete szerint ezek a mintázatok egy reakció-diffúzió folyamat eredményei. Ilyenkor az állati embrió bőrében két kémiai anyag létezik. Az egyik gátló, amely mind a saját maga, mind a másik anyag termelését akadályozza, míg a másik aktiváló, amely önmaga és a „partnere” termelését is elősegíti. Turing egy sor differenciálegyenletet vetett papírra, melyek a két kémiai anyag közti versenyt írják le. Az egyenlet paramétereinek módosításával az állat mintái is változnak. A főbb tényezők: mennyi aktiváló, ill. gátló anyag keletkezik, és hogy ezek milyen gyorsan terjednek szét. Turing kimutatta: a mintázat megjelenésének sarkalatos pontja, hogy a gátló anyag gyorsabban oszoljon szét az aktiválónál. 

Újabb kutatásokból kiderül: a bohóchaltól a leopárdig számos állat bőrszínmintái pigmentsejtek közti mikroszkopikus kölcsönhatásokból jönnek létre, s ezek valóban megfelelnek Turing egyenleteinek.

Michael Milinkovitch

Michel Milinkovitch evolúciós biológus professzor (Genfi Egyetem) biológusokból, fizikusokból és számítástudósokból álló csoportjával hasonlóan látványos állatra figyeltek fel: a Délnyugat-Európában honos pávaszemes gyíkra (Timon lepidus). A kutatók a Nature-ben írják le, hogy a pávaszemes gyík lassan alakítja ki felnőtt bőrszínét, méghozzá az egyedi bőrpikkelyek színének olyan számítási rendszer szerint való változtatásával, amelyet az 1940-es években egy másik matematikus, Neumann János talált ki. A svájci csapat kimutatta, hogy a gyík bőrpikkelyeinek geometriája a Turing-mechanizmust a Neumann féle számítási rendszerbe viszi át. Tehát e két matematikai óriás munkáját egyetlen biológiai kutatásban kapcsolják össze.

A kutatók arra lettek figyelmesek, hogy a fiatal, barna foltos gyík, ahogy felnő, fokozatosan alakítja ki bőrszínét, mígnem létrejön az a bonyolult, labirintusszerű minta, amelyben minden pikkely vagy zöld, vagy fekete. Ez a megfigyelés ellentmondásban állt a Turing-mechanizmussal, amely szerint a színes sejtek között mikroszkopikus interakciók történnek. Ahhoz, hogy megértsék, a mintázat miért a pikkelyek, és nem a biológiai sejtek szintjén alakul ki, két PhD-hallgató, Liana Manukyan és Sophie Montandon pávaszemes gyíkokat követett figyelemmel a fejlődésük 4 éve alatt a tojásból kikeléstől a teljes érettségig. Egy, a Milinkovitch-laboratóriumban korábban kifejlesztett igen nagy felbontású robotrendszer alkalmazásával több időpontra is rekonstruálták a pikkelyhálózatok geometriáját és színét.

Színváltó pikkelyek

A kutatók meglepődve látták, hogy miután a barna fiatalkori pikkelyek zöld vagy fekete színűvé válnak, továbbra is váltogatják színüket, zöldről feketére és viszont. Ez a nagyon furcsa megfigyelés arra késztette Milinkovitchot, hogy felvesse: a bőr pikkelyhálózata ún. „sejtautomata" lehet.

E számítási rendszert, melyben minden sejt változtatja az állapotát (jelen esetben színét), méghozzá a szomszédos sejtek állapotától (színétől) függően, Neumann János találta fel. 

Neumann János

Az elemeket sejteknek nevezzük, de nem kell, hogy biológiai sejteket képviseljenek. A gyík esetében az egyéni bőrpikkelyeknek felelnek meg. Ezeket az absztrakt automatákat széles körben használták természeti jelenségek modellezésére, de a Genfi Egyetem csapata fedezte fel egy, az élő szervezetben megjelenő valódi 2D automata első esetét. A négyéves színváltozás-elemzés alapján a svájci kutatók megerősítették Milinkovitch hipotézisét: a pikkelyek valóban a szomszédos pikkelyek színeitől függően változtak. A felfedezett matematikai szabályt végrehajtó számítógépes szimulációk olyan színmintákat hoztak létre, amelyek nem különböztethetők meg az igazi gyíkok mintáitól.

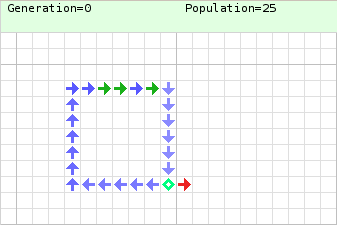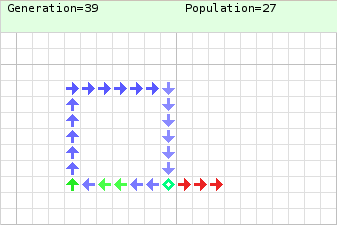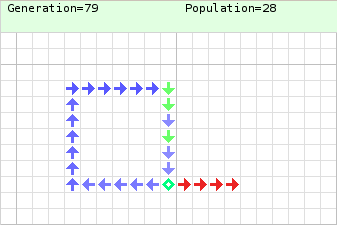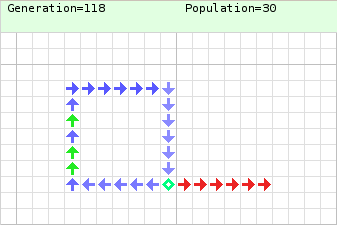Egyszerű konfiguráció Neumann sejtautomatájában

A pávaszemes gyík bőrén egy zöld sejtet átlagos esetben 2 zöld és 4 fekete vesz körül, egy feketét pedig 3 zöld, 3 fekete. Mindezt a pigmentsejtek interakciói önmagukban nem magyarázzák meg. 

Hogyan hozhatnak létre a pigmentsejtek közti, a Turing-egyenletek által leírt interakciók Neumann-automatát, amely pontosan illik a bőrpikkelyekre? A gyík bőre nem lapos: igen vékony a pikkelyek között, és jóval vastagabb a közepükön. Mivel a Turing-mechanizmus a sejtek mozgását tételezi fel, vagy a sejtek által keltett jelek szétterjedését, Milinkovitch arra jött rá, hogy a bőrvastagságnak ez a változékonysága hatással lehet a Turing-mechanizmusra. A kutatók el is végeztek számítógépes szimulációkat, amelyek a bőrvastagságra is kiterjedtek, és azt tapasztalták, hogy előáll a sejtautomata-viselkedés. Ez azt mutatta, hogy a sejtautomata, mint számítási rendszer nem csupán egy Neumann János által kifejlesztett absztrakt elképzelés, hanem egy, a biológiai evolúció által létrehozott természetes folyamatnak is megfelel.

Az automata viselkedése azonban tökéletlen volt, mivel Turing mechanizmusának és Neumann automatájának a matematikája nagyon különböző. Milinkovitch megkereste a 2010-ben Fields-érmet nyert matematikus professzort, Stanislav Smirnovot (Genfi Egyetem). Nem sok idő elteltével Smirnov a Turing-egyenletek ún. diszkretizálását szállította, amely formális kapcsolatot hozott létre ezen egyenletek és a Neumann-automata között. A kutatók Smirnov új egyenleteire alapuló számítógépes szimulációkkal olyan rendszerhez jutottak el, amely nem volt megkülönböztethető a Neumann-automatától. E rendkívül multidiszciplináris csapat így zárta le a kört ebben a csodálatos utazásban, a biológiától a kémián át a matematikáig ... és vissza a biológiáig.

Ford., szerk.: Jakabffy Éva