Az 1998. évi könyvhéten kiemelkedő érdeklődés kísérte Vámos Miklós új könyvét, melyből az átlagosnál jóval többet adtak el, és az utóbbi években ritkán látott módon több százan álltak sorba dedikálásért. A szerző maga sem titkolja, hogy sikerében jelentős része van „Lehetetlen” című televíziós műsorának, amelynek nézettsége néha a hárommilliót is elérte. A „Lehetetlen”-nek az volt az egyik mondanivalója, hogy lehetetlen nincs (csak esetleg az egyes emberek tehetetlenek). Bár a Vámos-műsor címét választottam e dolgozat címének, a műsortól eltérően azt kívánom megmutatni, hogy a matematikában a lehetetlennek éppoly fontos szerepe van, mint a lehetségesnek, és a lehetetlennel kapcsolatos kérdések a matematika legizgalmasabb fejezetei közé tartozhatnak.

Minden más tudománytól eltérően a matematikában ugyanis gyakran igazoljuk, hogy valami nem lehetséges, valami nincs. Mielőtt erre példákat mutatnánk a matematika történetéből, tekintsünk néhány egyszerűbb feladatot!

Három elemi feladat

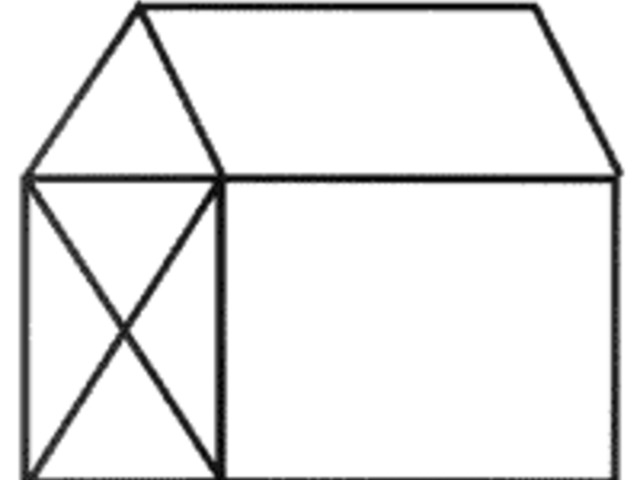
1. feladat.Újságok rejtvényoldalain gyakran találkozhatunk azzal a feladattal, hogy egy adott ábrát kell lerajzolni a ceruza felemelése nélkül. Például rajzoljuk le az 1. ábrát ilyen módon!

1. ábra. Megrajzolható-e egy vonallal a ceruza felemelése nélkül?

Több-kevesebb sikertelen próbálkozás után az emberben óhatatlanul felmerül a kérdés, hogy a feladat egyáltalán végrehajtható-e, és valóban, mint azt alább megmutatjuk, a fenti lerajzolás nem lehetséges. Itt tehát nem arról van szó, hogy mi nem tudjuk lerajzolni, vagy hogy eddig még senkinek sem sikerült ez, hanem arról, hogy felesleges is ilyet keresni, mert ilyen nincs.

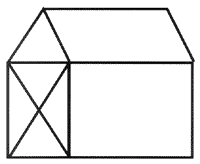
 2. ábra "Tologatós játék"

3. ábra. A "tologatós" játék az "1" és a "2" felcserélésével

2. feladat.Tekintsük a jól ismert tologatós (más néven tizenötös) játékot (2. ábra), amelynek egyes négyzeteit csúsztathatjuk, ha a szomszédos mező üres! A játék abból áll, hogy egy “összekevert” állásból kell az eredeti 1, 2, ..., 15 sorrendet visszaállítani. Mármost tételezzük fel, hogy valaki nem csúsztatásokkal állítja elő az “összekevert” állást, hanem kiszedi a kis négyzeteket, és azokat valamilyen sorrendben visszarakja. Például tételezzük fel, hogy úgy rakjuk őket vissza, hogy minden a helyére kerül, kivéve az 1-es és 2-es számú négyzeteket, amelyeket viszont megcserélünk (3. ábra). A kérdés az, hogy ekkor is elő tudjuk-e állítani az eredeti sorrendet a játék szerinti csúsztatásokkal.

  Mint látni fogjuk, ez a fenti konkrét esetben nem lehetséges.

3. feladat.Biztosan sokan ismerik a 4. ábrán látható tüske (más néven szoliter) játékot, amelynél egy lyukakat tartalmazó tábla bizonyos lyukaiba tüskéket teszünk, és a játék során egy tüskével (vízszintesen vagy függőlegesen) átugorhatunk egy mellette levő tüskét, feltéve, hogy annak másik oldalán szabad lyuk van, viszont a lépés során az átugrott tüskét le kell venni a tábláról (5. ábra). A játék különféle táblákon ismeretes, és általában az a cél, hogy a lehető legtöbb tüskét vegyük le a fenti módon.

4. ábra. A tüskejáték
 
5. ábra. A cél, hogy a lehető legtöbb tüskét vegyük le 

A mi feladatunk viszont kissé más, nevezetesen azt kérdezzük, hogy üres részre milyen messzire lehet eljutni a fenti játékban; pontosabban tételezzük fel, hogy a tábla mérete tetszőleges nagy, és a kezdeti tüskék mind egy adott vonalon vagy az alatt helyezkednek el (6. ábra). A kérdés az, hogy tetszőleges (általunk választott) kezdőállásból kiindulva milyen magasra tudunk a vonal fölé feljuttatni egy tüskét.

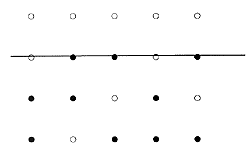6. ábra. A kezdeti tüskék helyzete és pontok megjelölése

Már az sem világos, hogy nem lehet akármilyen magasra feljuttatni, de hosszabb-rövidebb próbálgatás után rájövünk, hogy 4 magasra még sikerül tüskét feljuttatni, de 5 magasra sohasem, és valóban, az igazolandó, hogy teljesen mindegy, milyen kezdeti helyzetből indulunk ki és a játék során milyen stratégiát használunk, soha nem tudunk 5 magasra feljuttatni tüskét, azaz az adott vonal feletti 5. és magasabb sorokban levő lyukak mindig üresen maradnak (ez John Conway egy észrevétele).

  A fenti feladatokkal kapcsolatban megfogalmaztunk egy-egy lehetetlenségi állítást. De hogyan lehet ezeket igazolni? Például az 1. feladatnál elvben végignézhetnénk az összes lehetséges rajzolási módot, és megállapíthatnánk, hogy egyik sem jó. Bár ez az adott feladatnál lehetséges, bonyolultabb ábráknál ez nagyon időigényes lehet. A 2. feladatban már reménytelen végigpróbálni az összes lehetséges helyreállítási próbálkozást azok nagy száma miatt. A 3. feladatnál pedig már a szóba jöhető kezdeti konfigurációk száma is végtelen (végtelen táblát feltételezve), így azok végigpróbálása szóba sem jöhet.

  De akkor hogyan lehet a fenti állításokat igazolni? Egyáltalán hogyan lehet igazolni azt, hogy valami lehetetlen, nem létezik, nincs?

  Sokszor ez nem is olyan nehéz. Például az 1. feladatnál vegyük észre, hogy a rajzolás során, ha egy csomópontba beérünk, akkor onnan tovább is megyünk, ezért a csomópontokban a vonalak párosával kell, hogy szerepeljenek; kivéve persze a kezdő és végső csomópontot, ha azok nem ugyanazok, hiszen a kezdő csomópontban az induló vonalnak, a végső csomópontban pedig az érkező vonalnak nincs párja. Tehát ha egy ábra lerajzolható a ceruza felemelése nélkül, akkor vagy minden csomópontban páros sok vonal találkozik, vagy pedig két csomópont kivételével igaz ez. Mármost az 1. ábrán van három olyan csomópont, ahol három vonal, és van egy olyan csomópont, ahol öt vonal találkozik, tehát ebben az ábrában kettőnél több olyan csomópont van, ahol páratlan sok vonal találkozik, ezért ez az ábra nem rajzolható le.

A fenti megoldás teljesen univerzális, bármely (összefüggő) ábra akkor rajzolható le a ceruza felemelése nélkül, ha legfeljebb két olyan csomópont van benne, amelyeknél páratlan sok vonal találkozik; sőt azt is megadja, hogy ha van két ilyen csomópont, akkor a rajzolást feltétlenül az egyiknél kell kezdeni.

7. ábra. A négyzetek sorrendje

A második feladatnál egy adott állásban írjuk fel a kis négyzetek számait a 7. ábrán látható sorrendben. Tehát amikor minden mező a helyén van, akkor így az

S₁ := 1, 2, 3, 7, 6, 5, 4, 8, 9, 10, 11, 15, 14, 13, 12

sorrend adódik, míg a feladatban szereplő kiinduló állás sorrendje az

S₂ := 2, 1, 3, 7, 6, 5, 4, 8, 9, 10, 11, 15, 14, 13, 12.

  Az 1–15 számok tetszőleges sorrendjében számoljuk meg, hogy hány olyan számpárt találunk, amelynél egy nagyobb szám egy kisebb szám előtt áll, és nevezzük ezt a számot az adott sorrend indexének. Például S₁ sorrendnél ezek a számpárok a

(7, 6), (7, 5), (7, 4), (6, 5), (6, 4), (5, 4), (15, 14), (15, 13), (15, 12), (14, 13), (14, 12), (13, 12).

  Így ennek a sorrendnek az indexe 12, míg az S₂ sorrend indexe 13 a további (2, 1) pár miatt. Most tekintsük, hogy mi történik egy csúsztatásnál! Ha vízszintesen csúsztatunk, akkor a számok sorrendje egyáltalán nem változik meg, míg ha egy függőleges csúsztatást hajtunk végre, akkor a csúsztatott szám 0, 2, 4 vagy 6 hellyel kerülhet előrébb vagy hátrább. Könnyen látható, hogy eközben az index páros (pontosabban 0, 2, 4, 6) számmal változhat meg (például, ha a sorrend
..., a, b, x, y, z, u, c, d, ... volt, és ebből az ..., a, x, y, z, u, b, c, d, .... sorrend lett, akkor az index csak az {x,b}, {y,b}, {z,b}, {u,b} számpárok miatt változhat, és ezek miatt változik is, mert ha y < b, akkor a (b, y) párt számoltuk az első sorrendnél, de nem számoltuk a másodiknál, míg ha b < y, akkor fordítva, az (y, b) párt számoltuk a második sorrendnél, de nem számoltuk az elsőnél. Tehát összességében négy hely átugrásakor az index 0-val, 2-vel vagy 4-gyel nőhet vagy csökkenhet). Mivel a kiindulási S₂ sorrend indexe páratlan, és, mint azt éppen láttuk, az index csak páros számmal változhat, azt kapjuk, hogy csúsztatásoknál az S₂ sorrendből indulva csak olyan sorrendek érhetők el, amelyek indexe páratlan, így többek között az eredeti S₁ sorrend nem érhető el.

  Persze az teljesen érdektelen kérdés, hogy a 3. ábrán látható konfigurációból az eredeti (2. ábrán látható) konfiguráció visszakapható-e. Az igazán érdekes probléma az, hogy mely konfigurációkból kapható meg az eredeti, vagy másképpen fogalmazva az, hogy az eredetiből kiindulva mely konfigurációk érhetők el. A fenti gondolatmenet adja, hogy csak azok, amelyekhez rendelt sorrendben az index páros (hiszen az eredeti sorrend indexe páros), és megmutatható, hogy ez már meg is adja a pontos választ, mert a páros indexű konfigurációk mind meg is kaphatók. Így ahhoz, hogy eldöntsük, hogy egy tetszőlegesen összeállított kiindulási konfigurációból az eredeti visszaállítható-e, mindössze a hozzá rendelt sorrend indexét kell kiszámolnunk, és ha az páros, akkor az eredeti visszaállítható, ha pedig páratlan, akkor nem.

A fenti megoldás a lehetetlenségi bizonyítások egy sokszor alkalmazható elemét tartalmazza, az ún. invariáns ötletet. Mint láttuk, az egyes konfigurációkhoz hozzárendeltük az indexet, pontosabban annak a paritását, és egy csúsztatás során ez a paritás nem változott, invariáns maradt. Ezért egy kiindulási konfigurációból csak olyan más konfigurációk kaphatók meg, amelyekhez rendelt paritás ugyanaz, mint a kiindulásinál, és ez azonnal adta, hogy az eredeti állapot visszaállítása lehetetlen.

A harmadik feladat megoldása is egy ilyen jellegű ötlettel történhet, bár a megoldás jóval trükkösebb. Feltételezhetjük, hogy egy végtelen táblán játszunk, és az adott vonal felett az ötödik sorban kijelölünk egy O-val jelölt lyukat, ahova szeretnénk eljutni. Azt kell igazolni, hogy akármilyen konfigurációból indulunk is ki, amelyben a tüskék a vonalon vagy alatta vannak, ez nem lehetséges. Mármost a megoldás ötlete az alábbi: minden lyukhoz hozzárendelünk egy súlyt, és a tüskék egy tetszőleges állására összeadjuk azon lyukakhoz rendelt súlyokat, amelyekben tüske van; ez lesz az adott konfiguráció összsúlya. A súlyokat oly módon fogjuk megválasztani, hogy egy tüske átugrásánál az összsúly soha nem növekedhet, és még az is igaz lesz, hogy a vonalon ill. alatta levő összes súly S összege ugyanaz lesz, mint az O lyukban levő egyetlen súly nagysága. Ha mindez megvalósítható, akkor az O lyukba valóban nem juthatunk el, hiszen tetszőleges kezdeti konfigurációból indulunk is ki, annak összsúlya S-nél kisebb, így abból nem juthatunk el egy nagyobb összsúlyú konfigurációba, márpedig bármely konfiguráció, amely az O pontot tartalmazza, legalább S összsúlyú, hiszen már az O pont súlya is S.

A kérdés tehát az, hogy hogyan helyezzük el a súlyokat. Legyen q a q²+q = 1 egyenlet pozitív megoldása, azaz legyen
q=( 5–1)/2, és egy tetszőleges lyukhoz rendeljük hozzá a q^k súlyt, ahol k azt a számot jelöli, ahány lépést kell tennünk az adott lyuktól, hogy elérjünk az O lyukhoz (minden lépésben egyet léphetünk vízszintesen illetve függőlegesen, és emlékeztetünk arra, hogy pozitív k-ra q^k azt jelöli, hogy a q-t k-szor összeszorozzuk, míg q⁰=1). A 8. ábra mutatja az egyes lyukakhoz rendelt súlyokat.

8. ábra. A lyukakhoz rendelt súlyok

Könnyen látható, hogy egy tüske átugrása és levétele során a rendszer összsúlya nem nőhet. Ha például egy, az O-tól k távolságra levő tüskével ugorjuk át a mellette levő tüskét, és ha ekkor közeledünk az O ponthoz, akkor eredetileg az ugró és az átugrott pontokban levő tüskékhez rendelt súlyok összege q^k+q^k–1=q^k–2(q+q²) volt. Mármost az átugrás után e két tüske helyett egy tüskénk lesz az O ponttól k–2 távolságban, amelyhez rendelt súly q^k–2, ami a q²+q=1 egyenlőség miatt ugyanaz, mint az előbbi összeg. Hasonlóan látható, hogy az összsúly soha nem nőhet, és persze vannak olyan ugrások (ha távolodunk O-tól), amelyeknél csökkenhet.

Hogy a vonalon, ill. az alatta levő lyukak összsúlyát kiszámíthassuk, fel kell használnunk a mértani sor összegképletét:

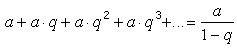
 Ezt a = q^j-vel alkalmazva látható, hogy bármelyik, a vonalon levő, és O-tól j távolságra levő lyuk, ill. az alatta, egy oszlopban levő lyukak összsúlya q^j/(1–q)·j = =5-re csak egy ilyen oszlop van, de j=6, 7, ...-re két-két ilyen oszlop található szimmetrikusan az O oszlopának két oldalán, ezért végül kapjuk, hogy a vonalon és az alatta levő lyukak összsúlya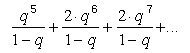

Ez utóbbi összegre ismét alkalmazhatjuk az (1) képletet az a = 2 · q⁶/(1–q) választással, így végül a kérdéses összsúly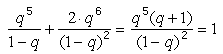

ahol az utolsó lépésben felhasználtuk, hogy q + 1 = 1/q és q² = 1–q. Tehát a kérdéses S összeg 1, ami pontosan az O lyukhoz rendelt súly, és éppen ezt kellett elérnünk.

Ha valaki többet akar olvasni hasonló játékokról, annak javaslom Csákány Béla élvezetesen megírt könyvét: Diszkrét matematikai játékok (Polygon Kiadó, 1998).