MindenTudás Egyeteme, 2008.

III. Véletlen gráfok és a sznobizmus

Térjünk rá arra a kérdésre, hogyan lehet egy nagyon nagy hálózathoz hasonlót csinálni kisebb méretben. Véletlenszerűen növekedő nagy hálózatok esetén működő ötlet lehet, ha megpróbálunk hasonló véletlen módszerrel létrehozni egy kisebb hálózatot. Így jutunk a véletlen gráfok elméletéhez. Ennek vizsgálatát Erdős Pál és Rényi Alfréd kezdték meg 1960 körül.

Az ő modelljükben rögzítünk n csúcsot, és ezek közé véletlenszerűen húzunk be éleket, amíg a kívánt sűrűséget el nem érjük. Az így kapott véletlen gráfokat sokat vizsgálták és sok érdekes tulajdonságot fedeztek fel velük kapcsolatban, de - mint látni fogjuk - az Erdős-Rényi-gráfok az internetet és más hasonló hálózatokat nem írják le elég jól.

1999-ben Barabási Albert-László és Albert Réka egy olyan modellt javasoltak, mely az internet fontos tulajdonságait (pl. fokszámainak eloszlását) jobban tükrözi. Az ő modelljükben nemcsak élek, hanem csúcsok is születnek, és egy új csúcs születésekor véletlenszerűen, de a fokszámokkal arányos valószínűséggel kiválaszt egy vagy több korábbi csúcsot, és ahhoz köti magát. Tehát azokat a csúcsokat, amelyek népszerűbbek, vagyis több szomszédjuk van, az új csúcs nagyobb valószínűséggel választja. Vagyis a véletlen gráf definíciójába sikerült beépíteni a sznobizmust! De milyen értelemben lesz ez jobb modellje pl. az internetnek?

A fokszámok tanulmányozása meglepő erdeményt hozott: az alábbi ábrán egy Erdős-Rényi-gráf fokszámainak statisztikája látható, a vízszintes tengelyen a lehetséges fokszámok vannak feltüntetve, az oszlopok magassága pedig azt mutatja, hogy a csúcsok hányadrészének a foka a vízszintes tengelyen szereplő érték. Az Erdős-Rényi-gráf fokszámeloszlása ún. haranggörbe alakú, vagy más szóval normális eloszlást mutat.

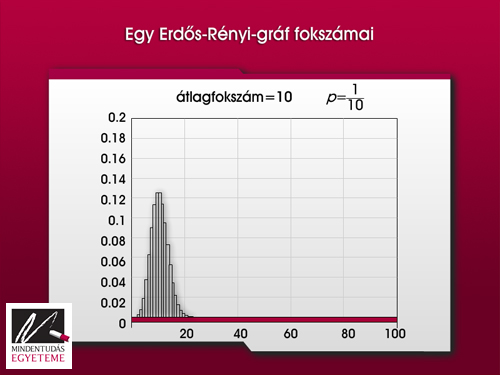
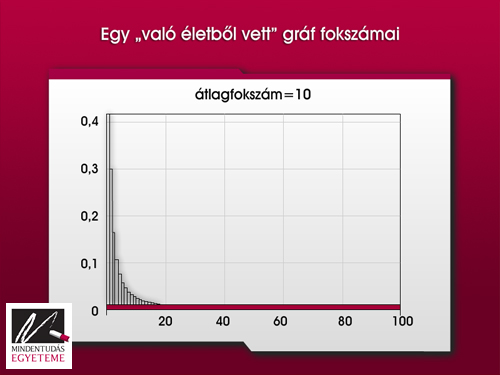
A valóságban előforduló hálózatok gráfjainak fokszámeloszlása azonban nem haranggörbére emlékeztet, hanem a fenti ábrán látható statisztikához hasonlít. Mindjárt két érdekes tulajdonságot is megfigyelhetünk: egyfelől a gyakoriság maximuma az elején van, vagyis a legkisebb fokszámú csúcsokból van a legtöbb, másfelől a fokszám statisztika a magasabb fokszámok felé haladva egyre lassabban cseng le. Matematikai kifejezéssel: a gyakoriság a fokszám valamilyen hatványa szerint csökken. A társadalomtudományokban már régebben felfedezték azt a jelenséget, hogy a ,,való életből vett” statisztikák igen gyakran ilyen elnyújtott, lassan lecsengő görbékre vezetnek; a jelenséget leírójáról, George Kingsley Zipf amerikai nyelvészről „Zipf-jelenségnek” is nevezik. Ilyen jellegű statisztikát mutatnak egy élettér fajainak egyedszámai, az egyes példányok mérete stb.

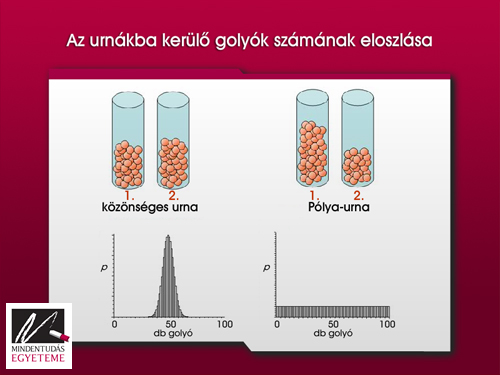
Hogy a Zipf-jelenség hátterét megértsük, ismerkedjünk meg a Pólya-urnával, amit Pólya György az 1920-as években vezetett be! Kétféle urnát láthatunk, az ún. közönséges- és a Pólya-urnát. A közönséges urnáknál (a baloldali piros edények) minden egyes golyó egyforma valószínűséggel esik az egyikbe vagy a másikba. A Pólya-urnák (a jobboldali kék edények) esetén az új golyó egy már korábban leesett golyót véletlenszerűen kiválaszt, és vele azonos edénybe pottyan (a sznobizmus tehát már ide is be van építve!). A kísérlet végén a 14. ábra tanúsága szerint a közönséges urnában közelítőleg ugyanannyi golyó lesz, amit a nagy számok törvénye alapján is elvárunk. Az első edénybe jutó golyók számának eloszlása az ismerős haranggörbét mutatja. A Pólya-urna esetén viszont egyforma valószínűséggel lesz 1, 2, 3, ... golyó az első edényben. A Pólya-urna magyarázza meg a Barabási-Albert-gráf tulajdonságait.

IV. A Szemerédi-féle regularitási lemma

Térjünk vissza a nagy hálózatokra. Hogyan tudnánk a szerkezetüket megérteni, kevés adattal leírni? Ehhez érdemes egy ábrázolásmóddal megismerkednünk. A rajznál néha többet mond (és természetesen számításokban jobban használható) az alábbi összekötöttségi táblázat. Hogy a gráf szerkezete még jobban látszódjon, helyettesítsük az 1-est fekete, a 0-t fehér négyzettel. Így a 16. ábrán látható, keresztrejtvényre emlékeztető rajzot kapunk.

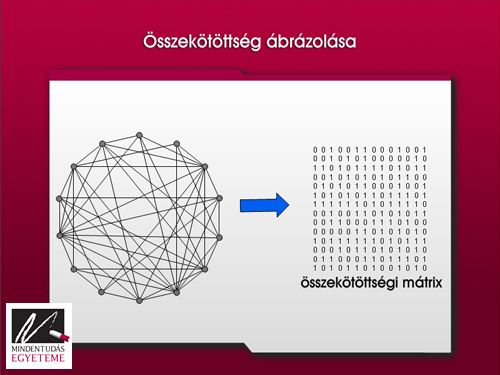
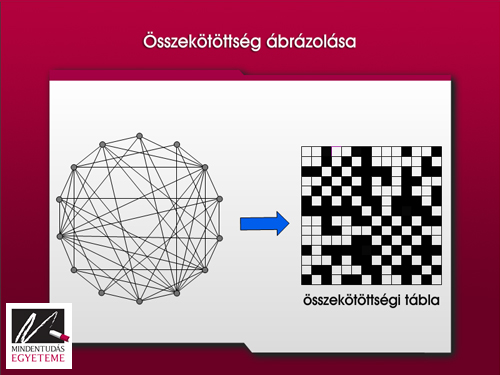
Ha ezzel az ábrázolási technikával egy olyan Erdős-Rényi-féle véletlen gráfot ábrázolunk, melyben a csúcspárok fele van összekötve, akkor „messziről nézve” az ábra egyenletesen szürkének fog látszani:

De vigyázzunk! Hiszen „messziről” a sakktábla-szerű elrendezés is egyenletesen szürkének látszik, ha nagyon sok sora van. Ha azonban itt a sorokat és oszlopokat átrendezzük úgy, hogy előrehozzuk a párosakat, akkor az  ábra jobboldalán látható sokkal szabályosabb, igen egyszerű struktúrát kapjuk:

Ezzel szemben egy véletlen gráf ábráját akárhogyan rendeznénk át, mindenképpen egyenletesen szürke volna. 

Itt az ideje, hogy bemutassuk a 20. századi magyar matematika egyik legnagyobb hatású eredményét, Szemerédi Endre regularitási lemmáját.

Az alábbi ábra bal felső sarkában látható gráfnak nem látszik különösebb struktúrája. Azonban a csúcsait alkalmasan átrendezve a jobb felső sarokban már azt látjuk, hogy az ábra négy különböző sűrűségű területre oszlik. Ezeken a területeken belül azonban már további struktúra nincs, ezek a részek már véletlenszerűek. A Szemerédi-lemma éppen ezt fogalmazza meg: minden gráf felbontható korlátos számú részre (ezek száma csak a hibahatártól függ, nem függ a gráftól) úgy, hogy a megfelelő kisebb négyzeteken a keresztrejtvény-ábra (kis hibával) véletlenszerű, más-más sűrűséggel. Ha ezeket a sűrűségeket ismerjük, a gráf sok fontos tulajdonságát meg tudjuk mondani.

V. Gigantikus hálózatok folytonos modellje

Végezetül arról ejtek néhány szót, hogyan lehet folytonosnak tekinteni egy kellőképpen nagy hálózatot. Ez egy 100 csúcsú gráf létrejöttét mutatja, mely úgy épül fel, hogy minden lépésben egy új csúcs és több új véletlen él születik, miközben az élek sűrűsége állandó marad. Az ábra egyre simább lesz. A fenti ábra 200 csúccsal mutatja be az előbbi módon megkonstruált gráfot. A jobb oldalon pedig az 1-max(x,y) függvénynek egy „szürkeskálás” ábrája látható. A kettő nagyon hasonló! És valóban: megmutatható, hogy ha 200 helyett 1000, 10000, stb. csúcsig mennénk el, a gráf „keresztrejtvény” ábrája egyre jobban hasonlítana a jobboldali „szürkeskálás” ábrához. A jobboldali függvény ismeretében a gráf sok lényeges tulajdonsága és paramétere egyszerű számolással meghatározható. A jobboldali függvény olyan közelítése a baloldali gráfnak, ahogyan a folytonosnak tekintett anyag közelítése a fématomokból álló kristálynak.

Szegedy Balázs fiatal kollégámmal megmutattuk, hogy egy nagyon nagy gráf lényegében mindig megközelíthető egy kétváltozós függvénnyel. Ez adott esetben egyszerűbb lehet, mint más leírás. Akkor hát melyik függvény írja le az internetet? Sajnos, erre a kérdésre a fenti elmélet nem ad értelmes választ, ugyanis sűrű gráfokra alkalmazható. Az internet-szerű hálózatokban sokkal kevesebb él van, egy csúcs csak a többi csúcs egy elenyészően kicsi hányadával van összekötve. Az internetet ily módon az azonosan 0 függvény igen jól megközelíti - ami viszont semmitmondó. Vannak bíztató eredmények az ilyen „ritka” hálózatokra vonatkozólag is, a teljes elméletre azonban még várni kell.

Kérdések, válaszok

Vajon az eukleidészi bizonyítás ma mekkora értékkel bír és változott-e a jelentősége a 2000 évvel ezelőtti képest? (Geller Tamás)

A bizonyítás ma is ugyanolyan jelentős fogalom a matematikában, mint 2000 éve. Természetesen az évszázadok folyamán sokat változott az a stílus, ahogyan a bizonyítást leírjuk, és változott (hullámzott) az is, hogy mennyire várjuk el, hogy minden részlet ki legyen fejtve. Ma már teljesen formalizálható az, hogy mi egy bizonyítás, és sokat fejlődött a matematika nyelve, jelölésrendszere. Gazdagodott a matematika azzal is, hogy a matematikai tevékenység eredménye nem csak a tétel plusz bizonyítás, hanem például egy algoritmus is lehet (bár ez sem új találmány: a legelső algoritmusok egyike az ókorból származó "Euklidészi Algoritmus"). 
Mindemellett a bizonyítás ma is a matematikai tevékenység gerince, sőt (ahogyan az előadásban megjegyeztem) sokkal fontosabb lett amiatt, hogy pl. egy program helyességét vagy egy rendszer biztonságát a matematika szabályai szerint kell(ene) bizonyítani.

Hogyan értékeli a formulamanipulációs software-ek (pl. Maple,MATHEMATICA) szerepét az "elméleti" (tiszta) matematika fejlődésében? Milyen várható hatása lehet e programoknak a matematika egyetemi oktatásában? (dr. Laczik Bálint)

Ezek a programcsomagok egyre több matematikus mindennapi eszköztárába tartoznak. Magam is, ha egy új kérdés vagy ötlet vetődik föl, egyre gyakrabban kezdem a gondolkodást azzal, hogy néhány egyszerű számítást  elvégzek. Ezzel a matematikában kialakul egy új terület, a "kísérleti matematika" (vagy pontosabban, mindennapossá és hatékonnyá válik egy olyan tevékenység, amely eddig is létezett és eredményes volt, de korlátozottan). A matematikus a számítógépet sokféleképpen használja: cikket ír, előadást illusztrál, kísérletezik. A közeljövőben ezek egyre inkább összefonódnak majd, és az említett programcsomagokkal, vagy hasonlókkal való kísérletezés egyre több előadásnak, egyetemi órának lesz része.

A materialista világképben létezik a véletlen, a valóságban véletlenek nincsenek: csak mi, emberek hisszük annak (www.andre.hu) Ön szerint?

Én inkább fordítva mondanám: sok olyan dolog, amire azt mondjuk, hogy "elvben kiszámítható", igazából véletlen, mert ha valami a világegyetem élettartamát meghaladó idő alatt számítható csak ki, akkor azt én nem nevezném kiszámíthatónak (hogy az "elvben" mit jelent, azt nem tudom értelmezni). Lehetnek persze olyan események (pl. egy radioaktív atom bomlása), amelyekben mindenki egyetért, hogy véletlenek.

A bonyolultságnak lehet-e más értelmezése is annál, mint amit Professzor úr említett? (doherty)

A bonyolultságnak sok fogalma van. Egy algoritmus bonyolultságát mérhetjük azzal, hogy (a bemenet méretének függvényében) egy-egy erőforrásból mennyit használ fel. Az előadásban az időt (pontosabban lépésszámot) tekintettem, ami a leggyakrabban használt bonyolultság-mérték. Gyakran van azonban szükség arra, hogy a tárfelhasználást, több processzor esetén a köztük való kommunikációt, egy nagy adatbázis használata esetén az adatbázisban való keresés mennyiségét tekintsük. Egy adathalmaz bonyolultságának fontos mértéke az előadásban említett információtartalom, amit az adathalmaz tömöríthetőségével mérhetünk, de más fontos mértékeket is tekintenek, pl. úgy, hogy a tömörítő algoritmusra a gyakorlati megvalósíthatóságot modellező feltevéseket tesznek. 
A különböző bonyolultsági mértékek között fontos, és csak kis részben tisztázott összefüggések vannak, melyek kutatásával a bonyolultságelmélet foglalkozik. Ezek közül  leghíresebb a "P-NP" probléma, mely egyike annak a 7 matematikai problémának, melyre a Clay Intézet az ezredforduló kapcsán egyenként 1 millió dolláros jutalmat tűzött ki. Lásd http://www.claymath.org/Millennium_Prize_Problems