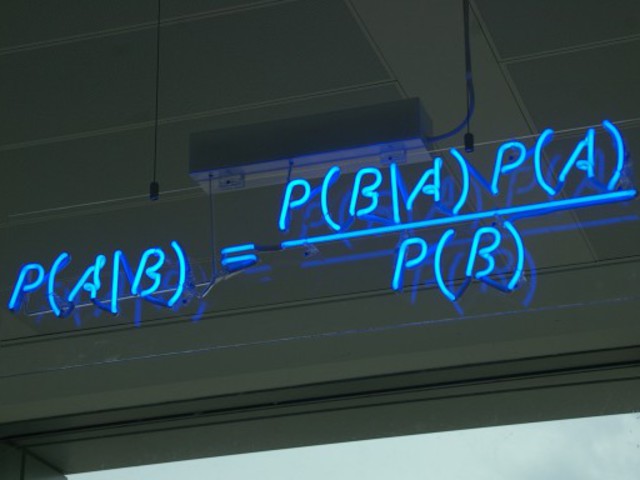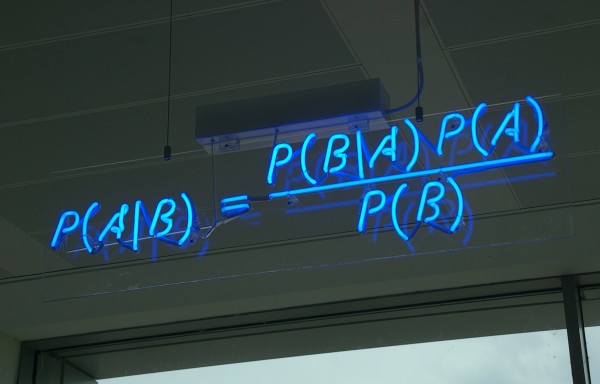Maroknyi adatból felderíteni a teljes igazságot, ez a tudósok, a nyomozók és a paranoiások álma. Utóbbiak egyike matematikai alapokra helyezi téveszméjét, és hozzáképzel egy 18. században élt lelkész-matematikust, a maga mágikus képletével, hogy igazságát megtámogassa. Ez a 20. századi Don Quijote azonban a 21. század tudományának forradalmát vetíti előre.

Őrületben a rendszer

Mekkora a valószínűsége annak, hogy valamelyikünk neves pszichológusok titkos kísérletének alanya legyen úgy, hogy nem is tud róla? Szinte semekkora. Egy középkorú férfi azonban, miután egyik különös esemény történt vele a másik után, arra a meggyőződésre jutott: ennek oka csakis pszichológusok kiterjedt összeesküvése lehet, és természetesen csakis őellene. Ilyesfajta téveszmével a fejükben sokan élnek, akár szabadlábon is, de ez a férfi különlegesen viszonyult saját összeesküvés-elméletéhez: matematikai eszközökkel akarta bizonyítani, hogy igaz. Pontosabban: hogy igen valószínű.

Beiratkozott hát egy pszichológiai kurzusra, hol máshol, mint a Harvard Egyetemen. Professzora felfigyelt a furcsa külsejű férfira, aki néhány alkalom után kirukkolt azzal, miért is jár be az előadásokra: olyan egybeesésekre lett figyelmes, mondta, amelyek nem lehetnek véletlenek.

Az egyik eset, amikor felesége szó szerint kimondta az ő gondolatait. Kis idővel ezután viszont az asszony bejelentette: válni akar.

A másik alkalommal kollégáival borozgattak, mígnem egyikük szóba hozta az elbocsátásokat. És lám, nem telt bele néhány nap: főnöke felmondott neki!

A férfi ilyen és hasonló balszerencsés fordulatok és zavaró egybeesések tucatjait élte át. Egyre inkább az a meggyőződés alakult ki benne, hogy pszichológusok hada kísérletezik vele a behaviorizmus vezető alakja, B. F. Skinner irányításával. (A történet a 70-es években játszódik.) Ezt kívánja bizonyítani, ezért jár az előadásokra. Azt is reméli, hogy a gyötrelmes pszichológiai kísérletnek egyszer vége szakad, és akkor ő mindennek kapcsán híres, befolyásos ember lehet.

A kurzus vége után néhány hónappal a tanítvány ismét jelentkezett a professzornál. Elmondta, hogy a kísérlet még mindig tart, és volt munkaadója pszichiáterhez küldte, hogy az igazolja: paranoiában szenved. A pszichiáter meg is állapította, hogy a férfinak téveszméi vannak. Például szentül hiszi, hogy a 18. században létezett egy lelkész, aki szabadidejében amatőr matematikusként alkotott egy elméletet arról, hogyan módosítja egy esemény valószínűségét más, kapcsolódó események megtörténte.

Az ő konkrét esetében a pszichológusok összeesküvésének kiinduló valószínűsége gyakorlatilag nulla. Viszont az új adatok, vagyis a furcsa egybeesések fényében ez módosul.

A férfi hosszú, matematikai képletekkel teletűzdelt halandzsát írt a bíróságnak azzal a végkövetkeztetéssel, hogy saját összeesküvés-elméletének valószínűsége nem kisebb, mint 999 999 : 1 000 000.

Harvardi professzorát azért hívta fel, hogy tanúskodjon mellette a bíróságon: a lelkész-matematikus nemcsak az ő kitalációja. A professzor készséggel megtette, és jó oka volt rá: ezúttal az őrültnek volt igaza. No nem a titkos összeesküvésben, csak abban, hogy a rejtélyes matematikus valóban létezett. 1701-ben született Londonban, és Thomas Bayesnek hívták. Tétele azt mutatja meg, hogyan terjeszthető ki a valószínűségszámítás az egymástól független eseményekről azokra, amelyek kapcsolódnak. Vagyis a feltételes valószínűséget.

A professzor mindezt ismertette tanúvallomásában. Ennél többet természetesen ő sem tehetett tanítványáért.

A szerény kezdetektől…

Ma már nem kellene tanúvallomás Bayes létének igazolásához. Ám nem véletlen, hogy a hírnév az ő esetében két és fél évszázadot késett: ez a mára a tudományban ikonná vált figura a maga idejében igen szerényen viszonyult saját tálentumához. Amit barátai is igazolnak. Köztük a Bayes-tételt közzétevő Richard Price matematikus-lelkész, aki viszont Benjamin Franklinnak is barátja volt. Ő úgy írja le Bayest, mint az egyik legzseniálisabb embert, akit valaha ismert. Bayes nemcsak a matematikában volt járatos, hanem a filozófiában, elektromosságban, optikában, zenei harmóniában és égi mechanikában is.

Bár tagjává választotta a Royal Society (Brit Tudományos Akadémia), tudományos munkáját alapvetően saját örömére végezte, nem törődve neve feltüntetésével. 1748-ban felvázolt formuláját Price olvasta fel a Royal Societyben 1763. karácsonya előtt, Tanulmány a valószínűség tana egyik problémájának megoldásáról címmel.

… a tudományok forradalmáig

A képlet oly egyszerű, hogy középiskolás fokon is igazolható. Sokáig, mint megalkotója, ő sem keltett feltűnést: valószínűségszámítás-könyvekben és diákok segédleteiben, a tangens tétel és hasonlók társaságában aludta Csipkerózsika-álmát. Hogy a tudomány hány területének ad majd új lendületet, azon bizonyára Bayes csodálkozott volna a legjobban.

Stanislas Dehaene kortárs pszichológus professzor (Collège de France), a Számérzék és más ismeretterjesztő bestsellerek szerzője a Bayes-tétel mai térhódítása kapcsán valóságos forradalomról beszél. Nem véletlen, hogy kurzust is tart erről A bayesi forradalom a kognitív tudományokban címmel, s mindjárt kétéveset. De mi lehet ezen egyszerű képlet titka, ami miatt az utóbbi évtizedben egyszerre bukkan fel olyan, egymástól távoli területeken, mint az idegtudomány és a részecskefizika, a csillagászat és az orvosi diagnosztika, vagy éppen a klímakutatás és a genetika?

Stanislas Dehaene

A Bayes-képlet akkor válik igazi ütőkártyává, ha a kérdéses jelenség sok tényező összjátékától függ, illetve ha információink gyérek vagy bizonytalanok. Ez a helyzet például a részben genetikai eredetű betegségeknél, amelyek óriási többségét a DNS-en bekövetkezett apró elváltozások százai idézik elő. Mármost ha adott állapot n számú rejtett paramétertől függ, amelyek mindegyike csak 0 és 1 értéket vehet fel, az okokra hagyományos statisztikával csak 2n számú, egymást követő megfigyelés után derülhet fény. Amennyiben egy rákfajta beindításában 100 gén játszik szerepet, ezek azonosításához 2100 számú beteg géntérképét kellene elkészítenünk.

Annak tudatában, hogy az egyének között milliónyi genetikai eltérés mutatkozik, hogyan is találhatnánk meg azokat a veszélyes elváltozás-együtteseket, amelyeket látva elmondható: adott személynek bizony mindent el kell követnie a cukorbaj, a szívinfarktus vagy a rheumatoid arthritis (ízületi gyulladás) megelőzésére? Bayesi statisztikával ez sem reménytelen. A bostoni Robert Plenge erre alapozva alkotta meg modelljét, amely alkalmas lehet annak kimutatására, melyek a kockázatos kombinációk.

A képlet, amely megfejti a világot…

Ha a lehetséges okok sokfélék, és kibogozhatatlanul összefonódnak, már több bayesi formulára van szükség, akár sok százra is. Judea Pearl amerikai matematikus már a 80-as években kimutatta, ezekkel felfejthetjük az összefüggő okok hálózatát. Ma már rendelkezésre állnak a bayesi hálózatok programkódjait futtató számítógépek. A bayesi hálózatok erőssége, hogy a megfigyelések hézagait szakértői adatokkal töltik ki.

A tudományos haladással egyre tágul az ismeretlenek mezője. A képlet, amely magát a tudományos alázatot fejezi ki, s egy olyan tudomány lényegét, amely belátja magáról, hogy saját tárgya már meghaladta, méltó a harmadik évezredhez. A mai kutatókat foglalkoztató legfőbb problémák egymásba szövődő ok-hálózatokkal jelentkeznek. A Bayes-képlet ma csillagok születésének mechanizmusait tárja fel, a jövő évtizedek hőmérséklet-emelkedéseit becsüli meg, fajok evolúciójára derít fényt. Sőt lehet, hogy koponyánkba is bevilágít.

… és gondolkodásunknak is kulcsa?

Mindannyiunk agyában ott lakik egy kis Thomas Bayes, mondja Stanislas Dehaene. Ezen intuitív francia kutató már megtalálta a számérzék helyét agyunkban, a jobb oldali fali lebenyben. De hol lehet akkor Bayes? Nagyon úgy tűnik, hogy mindenütt. Legalábbis elménk számos tevékenységében.

Nem minden nap látunk ilyet, állítja Dehaene, hogy ennyire hirtelen felbukkan egy elméleti keret, amely a tudományág összes területébe beszüremkedik. Jó páran gondoltuk, hogy a kogníciónak nincs általános elmélete: az az evolúció barkácsolásának eredménye, ám ezt a nézetet romba dönti a bayesi statisztika.

Ránézésre a tiszteletes képlete távol esik elménk működéseitől, színtiszta matematika. Ám Dehaene szerint e matematikában éppen hogy gondolkodásunk tükröződik. A képlet absztrakt öltözéke jellegzetesen emberi mechanizmust rejt: annak ellenállhatatlan igyekezetét, hogy információk szűkében is kibányásszuk az okokat. Ezen algoritmus, amely új adatok alapján szüntelenül napra készre hozza azt, amit már tudunk, valóságos gondolkodómotor. Kiderül: az agy bayesi módon modellezi egy sosem látott esemény kimenetelének valószínűségét. S ez a képesség korai gyermekkorunktól be van élesítve!

Bayes-bébik

A 20. századot uraló elképzelés szerint iskoláskornál fiatalabb gyermekek képtelenek logikai következtetésre, konkrétak és egocentrikusak. Mára merőben másként látjuk: a gyermekek képesek a racionális jóslásra, és ez a fajta okoskodás már a szóbeliség kialakulása előtt meglepően gazdag és hatékony.

Téglás Ernő pszichológus (Közép-Európai Egyetem Kognitív Fejlődéstani Kutatóközpontja) 2011-es kísérletében babáknak vetít rövid filmet: lefelé nyíló, lottósorsolóhoz hasonló gömbben színes tárgyak mozognak: három egyforma lyukas sárga kocka és egy kék figura. A gömb tartalmát néhány másodpercre eltakarják, majd az egyik tárgy kipottyan a gömb alján. Mennyire érdekli ez a babákat?

Attól függ, sikerül-e meglepni őket. Ezt azzal díjazzák a babák, hogy hosszasan bámulják a jelenetet, nem kalandoznak el. Téglás babái felfigyelnek, ha a takarási idő szinte csak egy pillanat, mégis egy előzőleg a nyílástól távol eső tárgy hullik ki. Ez nem felel meg elvárásaiknak. Ha a takarási idő hosszabb, 2 másodperc, a babák szempontot váltanak. Akkor lepődnek meg, ha az egyetlen kék figura esik ki, hiszen ez valószínűtlenebb, mint ha „közönséges” sárga kocka érkezne. 1 másodperces takarásnál a távolság és a ritkaság is számít.

A kutatóknak bayesi ideális megfigyelő modellel sikerült megjósolni a babák nézési időit. A gyermekek tárgyak mozgásával kapcsolatos számításai egyszerre veszik figyelembe a teret, az időt és a tárgyak gyakoriságát, sőt azt is, melyik éppen a fontosabb szempont.

Mire jó, hogy születéstől bayesi statisztikusok vagyunk? Óriási előny! Jóval kevesebb a tapasztalatunk, mint a nagyoknak, mégis hamar ki tudjuk számolni, minek is kéne történnie körülöttünk.

Kezdetben vala a bayesi statisztika

Még csak most ismerkedünk vele, mégis el kell fogadnunk, hogy első levegővételünktől, vagy még korábbtól velünk volt. A klasszikus statisztikát vélnénk természetesebbnek, de mi sem áll távolabb a gyermekektől. Óvodáskorukra sem hajlandók másképp következtetni, csakis bayesi okoskodással.

A karizmatikus kaliforniai pszichológusnő, Alison Gopnik (Berkeley Egyetem) különleges csodálattal viseltetik a AAgyermekek, mint ösztönös, és természetesen bayesiánus tudósok iránt. Akárcsak ő, a kísérlete is szellemes.

Alison Gopnik

Egy érzékeny plüssmajomnak ellenállhatatlanul tüsszögnie kell egy bizonyos színű virágtól. A 4 éveseknek azt kell kideríteni, melyiktől. Sárga és piros virág jön, és a majom tüsszög. Lila és sárga: tüsszög. Lila és piros: nem tüsszög. Melyik virág ingerli a majmot? A gyerekek rávágják: a sárga. A klasszikus valószínűségek itt nem számítanak, hisz azok alapján a majom az esetek felében a lila és a piros virágtól is tüsszög. Az okok összekapcsolásával, bayesi úton juthattak csak el a gyerekek a tüsszögés okáig.

Ha a virágok nem párban, hanem külön-külön tűnnek fel, nincs mit összekapcsolni, nem segít a bayesi logika. Hogyan következtetnek a gyermekek? Klasszikus módon? Nem, azt már nem. A véletlenre bízzák: random módon mondanak sárgát, lilát, pirosat, mert még nem képesek a szokásos gyakorisági törvényekkel kalkulálni. Akkor sem, ha nincs más megoldás.

Bayesi agyak…

Lehet-e, hogy nem csupán egy kis Bayes ül az agyunkban, hanem hogy maga az agy is bayesi hálózat? Hogy a képlet nemcsak leírja gondolkodásunkat, hanem a gondolkodás szervének alapvető szerkezeti elve?

Ha kevés adatból kell gyorsan következtetni, az esetek többségében a bayesi agy jár jól. Ezért nem lehetetlen, hogy az evolúció is előnyben részesítette a bayesi idegsejt-hálózatokat.

Sophie Denève neurológus (École normale supérieure, Párizs) szerint idegrendszerünk bonyolult világban fejlődik, elképesztő zajjal zavart jeleket kap, így folyton megközelítésekkel kell élnie, hogy kezelhesse a bizonytalanságokat. E téren a bayesi jóslás behozhatatlan előnnyel rendelkezik. Az agy, mondja Dehaene, e jósló rendszerrel javítja fel az érzékszervek útján nyert bemeneteket.

Számos kutató MRI-vel nyomoz az agyban megbúvó Bayes után, s már látják a tanújeleket. A Carnegie Mellon University (USA) kutatói felfedezték: egyes idegsejtek még azelőtt küldenek jeleket, hogy az érzékszervekből bármi jött volna. Úgy tűnik, az idegsejtek éppen jóslásba bocsátkoznak: milyen esemény várható a bayesi szabályok szerint.

Számunkra a világ valószínűségek olyan gyűjteménye, amelyet állandóan frissítünk észleléseink alapján; olyan információk gigantikus sokasága, amelyeket egy 18. századi tiszteletes törvényei irányítanak.

…és anti-bayesi gondolkodás?  

Áthatja a tudományt, az elménket, sőt egyre inkább a robotokat is, amelyek bayesi alapokon egyre gördülékenyebbekké válnak. A mesterséges intelligenciák eddig sem álltak rosszul sakkban; de hogy egy android legalább olyan ügyesen mozgassa a bábukat a táblán, mint akár egy ötéves gyermek? A hagyományos programok által vezérelt robotok csak akkor ismernek fel egy alakot, ha világos képet kapnak róla érzékelőik útján, majd megállapítják, azonosítható-e valamely tárggyal az adatbázisukban. A bayesi automaták ellenben hasznosítják a töredékinformációt is, azt egybevetik adatbázisuk összes elemével, minden társításhoz hozzárendelve egy valószínűséget. A legvalószínűbb tárgyat azután „felismerik”, akár szűrt fényben is. Így képesek kikerülni váratlan akadályokat, vagy megérezni olyan anyagokat is, amelyek még nem szerepelnek adatbázisukban.

A bayesi spam-szűrők folyamatosan „tanulnak” az újabb és újabb esetekből, így együtt fejlődnek a trükközőkkel.

A keresztül-kasul bayesi világnál csak egy az érdekesebb: amikor képtelenek vagyunk a bayesi következtetésre, noha éppen arra lenne szükség. Talán túl ostobák vagyunk? Nem erről van szó: a tévedésnek szakértők, matematikusok, orvosok és jogászok is áldozatul esnek.

A leghíresebb a Monty Hall probléma. Ez a nevét egy ismert TV-s vetélkedő, a Let’s Make a Deal (Kössünk üzletet) műsorvezetőjéről kapta. A showt 1963-76, majd 1980-91 között sugározták, és fő vonzerejét a jóképű műsorvezető, Monty Hall és kihívó segítője, Carol Merrill, a 1957-es Miss Azusa (Kalifornia) adták. A műsor magyar változatát Zsákbamacska címmel Rózsa György vezette.

Kedves Olvasó, képzelje magát a játékos helyébe, akinek Monty Hall a következőket mondja:

Gratulálunk! Ön a játék utolsó szakaszához érkezett, és immár karnyújtásnyira van a fődíjtól, egy vadonatúj, piros sportkocsitól, amelyet az Ön előtt látható három ajtó egyike mögé rejtettünk. A másik két ajtó mögött két imádnivaló kecske vár. Önnek nincs más dolga, mint helyesen választani! Nos, melyik ajtó mögött érzi a valódi lóerőket?

Tehát, kedves versenyző, az egyest választotta? Érdekes döntés. Megkérdezhetem, miért? Bár tudja mit, hagyjuk, maga olyan szimpatikus nekem, és nem szeretném, ha üres kézzel távozna. Mivel én tudom, melyik ajtó mit rejt, segítek egy kicsit. Mit szólna, ha kinyitnám az Ön által nem választott két ajtó valamelyikét? Hátha akkor meggondolja magát! Tudja mit, ki is nyitom, legyen mondjuk a kettes!

Áhá! Kecske! Fordítsuk akkor komolyra a szót. Adok Önnek még egy lehetőséget. Ha akarja, meggondolhatja magát és változtathat. Csak egy szavába kerül, és átmehet a hármasra. Vagy kitart eredeti döntése mellett, és megnézzük, helyes volt-e. Nos, mit választ?

Hogy az Olvasó úgy döntött-e, ahogy a legtöbb ember; vagy úgy, ahogy a most 100. évfordulós Erdős Pál, a híres matematikus tette volna? Vagy épp ahogy a madarak, például a galambok? A folytatásból kiderül. 

Jakabffy Éva