Ma 140 éve született Kőnig Dénes, az első gráfelméleti tankönyv szerzője

Lovász László Kőnigről:

„Kőnig Dénes, a 20. század első felében alkotó nagy magyar matematikus volt az, aki elkezdte ezt a területet vizsgálni, s először ért el fontos eredményeket. Az első gráfelméleti tankönyvet is ő írta 1937-ben. Tanítványai a korszak legkiválóbb matematikusai voltak - ebből a generációból Erdős Pál nevét az egész világ megismerte, de mellette Gallai Tibor vagy a nem főállású ’gráfelmélészek’, Turán Pál, Hajós György is komoly eredményeket produkáltak. Épp ezért nálunk sokkal előbb lett elfogadott ez a tudományterület, mint a világ más országaiban.”

„A matematikán belül a 19. századig az analízis, a differenciál- és integrálszámítás hozta a nagy fejlődést – ezt folytonos matematikának lehet röviden nevezni. Közben alakulgatott egy másik ág, a diszkrét matematika is, de elég lassan. A diszkrét matematikát szokás végesnek is nevezni, mert nem folytonos, hanem egymástól elkülönített elemekből álló struktúrákat vizsgál, például egy hálózatot. A diszkrét matematika, illetve a gráfelmélet – ami a hálózatelmélet matematikai alapja – Magyarországon különösen erős volt, mert Kőnig Dénes, majd később Erdős Pál hatására nagyon sokan foglalkoztak ezzel.”

Recski András (BME VIK, Számítástudományi és Információelméleti tanszék):

„Nemcsak a tudományos világ, hanem a mai fiatalok előtt is példaként szolgálhat a munkássága annak a műegyetemi professzornak, akit a fiataloknak mutattam be előadásomban. Kőnig Dénes nemcsak a BME-n, hanem a világon is elsőként tartott önálló egyetemi kurzust a gráfelméletről, emellett ő a szerzője a világ első gráfelméletről szóló könyvének is. A professzor iskolateremtő hatása, jelentős tudománynépszerűsítő tevékenysége máig érezhető a magyar matematikában, eredményei alapvető fontosságúak a gráfelméletben, több tétele a matematikai, a villamosmérnöki, valamint a mérnök-informatikai alapképzés fontos részét képezi.”

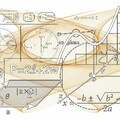
„Kőnig Dénes egyik legkiemelkedőbb eredménye az ún. hozzárendelési probléma gyors és hatékony megoldására adott algoritmusa. Gyakorlati példa: egy műhelyben szét kell osztani a dolgozók között az elvégzendő, egy személyes és egy napos feladatokat úgy, hogy nem minden munkás képes tetszőleges feladat elvégzésére. Tegyük fel, hogy 5 feladatot szükséges felosztani 6 munkás között úgy, hogy az első munkás csak az első két feladathoz, a második csak az első három feladathoz ért, …, míg a hatodik dolgozó csak a harmadik és a negyedik feladatot tudja elvégezni. Ekkor a pontos helyzetet a lenti ábrán látható ún. páros gráf szemlélteti. A feladatok és a munkások az „A” és a „B” halmazok pontjai, a köztük lévő élek pedig az egyes feladatokhoz kapcsolódó szakértelmeket jelzik. A feladat egy lehetséges megoldását a vastag, piros vonalak szemléltetik. „Általánosan fogalmazva, „a” mennyiségű feladat és „b” számú dolgozó esetén az összes lehetőségek száma elvileg akár b X (b–1) X … X (b–a+1) is lehetne. Ezek gépies végigpróbálása még a leggyorsabb számítógépeknek is évmilliókig tartana, ha „a” és „b” kellően nagy, legalább 60-80 körüli érték. Kőnig Dénes a problémára egy olyan algoritmust alkotott meg, amelyet egy átlagos számítógép is gyorsan végrehajt még akkor is, ha „a” és „b” értéke akár több ezer.”

Kőnig Dénes professzor munkássága többeket inspirált: köztük tanítványát, Gallai Tibort, (1912-1992) akinek egyes gráfelméleti eredményeit a BME-n jelenleg is zajló diszkrét matematikai kutatásoknál is alkalmazzák. Gallai algoritmusa az informatikai és villamosmérnöki ipari alkalmazásokat is segíti: egyik tételét például integrált áramköri chip-ek tervezésénél, a többrétegű huzalozásnál is alkalmazzák. Mellette Kőnig Dénes olyan neves matematikusokra is nagy hatást gyakorolt, mint Erdős Pál, Klein Eszter, Szekeres György vagy Turán Pál, akiknek későbbi munkásságában a gráfelmélet és a diszkrét matematika is jelentős szerepet kapott. Ez a terület egyébként a nemzetközi berkekben is nagyra tartott magyar matematika egyik legsikeresebb ága, többek között az Abel-díjat nyert Szemerédi Endre és Lovász László legfontosabb kutatási eredményei is ide sorolhatók.

Életrajz

Kőnig Dénes (Budapest, 1884. szeptember 21. - Budapest, 1944. október 19.) magyar matematikus, a Műegyetem rendkívüli professzora. Kőnig Gyula matematikus és Oppenheim Erzsébet gyermekeként született. Matematikát 1902-től a budapesti és a göttingeni egyetemen tanult; Göttingenben nagy hatással volt rá Minkowski négyszínsejtésről szóló előadása. 1907-ben a Budapesti Műszaki Egyetemen Kürschák József témavezetésével doktorált. Először gyakornokként dolgozott a Műszaki Egyetemen, majd 1908-tól tanársegédként, 1910-ben adjunktus lett. 1911-től magántanárként nomográfiát, analízist és halmazelméletet tanított, 1913-tól meghívott előadóként működött. 1932-ben rendkívüli tanárrá, 1935-ben pedig professzorrá nevezték ki. Gallai Tibor szakdolgozatának témavezetője volt. A gráfelmélet mellett elsősorban topológiával foglalkozott. A második világháború alatt az üldözött matematikusokat segítette; a nyilas hatalomátvétel után öngyilkos lett; a Horthy Miklós (ma Bartók Béla) utca 28. szám alatti lakásából leugorva szerzett agysérülésbe halt bele.